

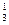 ·0.81·(1-0.8)2=0.096; 恰有2次击中9环以上,概率为p2=C
·0.81·(1-0.8)2=0.096; 恰有2次击中9环以上,概率为p2=C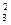 ·0.82·(1-0.8)1=0.384;
·0.82·(1-0.8)1=0.384; 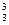 ·0.83·(1-0.8)0=0.512. 因为上述三个事件互斥,所以甲运动员射击3次,至少1次击中9环以上的概率p= p1+ p2+ p3=0.992.
·0.83·(1-0.8)0=0.512. 因为上述三个事件互斥,所以甲运动员射击3次,至少1次击中9环以上的概率p= p1+ p2+ p3=0.992. 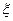 表示2次射击击中9环以上的次数,所以
表示2次射击击中9环以上的次数,所以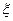 的可能取值是0,1,2.
的可能取值是0,1,2. 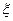 =2)=0.8·0.75=0.6; P(
=2)=0.8·0.75=0.6; P(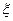 =1)=0.8·(1-0.75)+(1-0.8)·0.75=0.35;
=1)=0.8·(1-0.75)+(1-0.8)·0.75=0.35;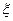 =0)=(1-0.8)·(1-0.75)=0.05. 所以
=0)=(1-0.8)·(1-0.75)=0.05. 所以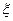 的分布列是
的分布列是| ξ | 0 | 1 | 2 |
| P | 0.05 | 0.35 | 0.6 |
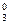 ·0.80·(1-0.8)3=0.008.
·0.80·(1-0.8)3=0.008.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题



序号 (i) | 分组 (睡眠时间) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [4,5) | 4.5 | 6 | 0.12 |
| 2 | [5,6) | 5.5 | 10 | 0.2 |
| 3 | [6,7) | 6.5 | 20 | 0.4 |
| 4 | [7,8) | 7.5 | 10 | 0.2 |
| 5 | [8,9] | 8.5 | 4 | 0.08 |


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )
) 的人数;
的人数; 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
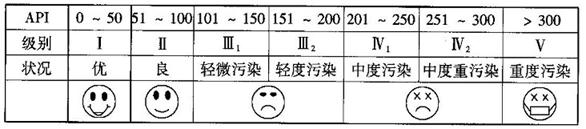
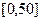 ,
,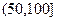 ,
,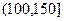 ,
,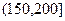 ,
,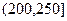 ,
,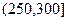 进行分组,得到频率分布直方图如图5.
进行分组,得到频率分布直方图如图5. 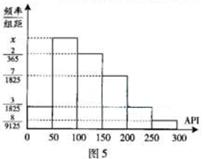
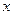 的值;
的值;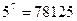 ,
,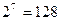 ,
,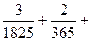
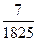
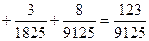 ,
,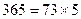 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分&6bsp;&6bsp;&6bsp;组 | 频数 | 频率 | 频率 组距 |
| [382,222) | |||
| [222,222) | |||
| [222,242) | |||
| [242,262) | |||
| [262,282) | |||
| [282,322) | |||
| [322,322) | |||
| [322,342] | |||
| 合&6bsp;&6bsp;计 | 2.25 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.65,65 | B.70,65 | C.65,50 | D.70,50 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com