
在∆ABC中,tanA是以-4为第三项,4为第七项的等差数列的公差,tanB是以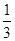 为第三项,9为第六项的等比数列的公比,则这个三角形是
为第三项,9为第六项的等比数列的公比,则这个三角形是
| A.钝角三角形 | B.锐角三角形 | C.等腰直角三角形 | D.以上都不对 |
B
解析试题分析:以数列为背景,建立得到角的关系式,进而结合两角和差的三角函数关系式,得到A+B的值, 进而得到三角形的形状。
因为tanA是以-4为第三项,4为第七项的等差数列的公差,则等差数列的通项公式可知,4-(-4)=4tanA,tanA=2,
根据tanB是以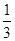 为第三项,9为第六项的等比数列的公比,则由等比数列的通项公式可知
为第三项,9为第六项的等比数列的公比,则由等比数列的通项公式可知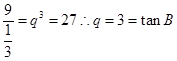 ,而tan(A+B)=
,而tan(A+B)= 
根据A,C,B的正切值为正数,说明了都是锐角,因此可知选B.
考点:本试题主要是考查了等差数列和等比数列的通项公式。
点评:确定三角形的形状问题,一般先由已知得到角的关系式,或者是边的关系时候,然后化简分析得到结论,同时要结合三角函数的公式来化简,体现了三角与数列的知识交汇运用。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com