
某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段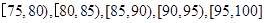 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
(Ⅰ)6,(Ⅱ)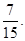
解析试题分析:(Ⅰ)根据频率分布直方图中小长方形面积为频率,而频数为总数与频率之积. 因此参加社区服务在时间段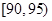 的学生人数为
的学生人数为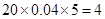 (人),参加社区服务在时间段
(人),参加社区服务在时间段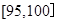 的学生人数为
的学生人数为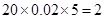 (人).所以参加社区服务时间不少于90小时的学生人数为
(人).所以参加社区服务时间不少于90小时的学生人数为 (人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件
(人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件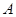 .由(Ⅰ)可知,参加社区服务在时间段
.由(Ⅰ)可知,参加社区服务在时间段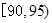 的学生有4人,记为
的学生有4人,记为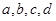 ;参加社区服务在时间段
;参加社区服务在时间段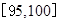 的学生有2人,记为
的学生有2人,记为 .从这6人中任意选取2人有
.从这6人中任意选取2人有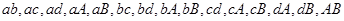 共15种情况.事件
共15种情况.事件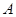 包括
包括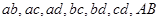 共7种情况.所以所选学生的服务时间在同一时间段内的概率
共7种情况.所以所选学生的服务时间在同一时间段内的概率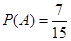 .
.
解:(Ⅰ)由题意可知,
参加社区服务在时间段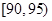 的学生人数为
的学生人数为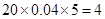 (人),
(人),
参加社区服务在时间段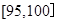 的学生人数为
的学生人数为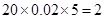 (人).
(人).
所以参加社区服务时间不少于90小时的学生人数为 (人). 5分
(人). 5分
(Ⅱ)设所选学生的参加服务时间在同一时间段内为事件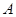 .
.
由(Ⅰ)可知,
参加社区服务在时间段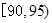 的学生有4人,记为
的学生有4人,记为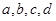 ;
;
参加社区服务在时间段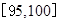 的学生有2人,记为
的学生有2人,记为 .
.
从这6人中任意选取2人有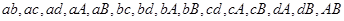 共15种情况.
共15种情况.
事件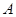 包括
包括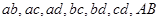 共7种情况.
共7种情况.
所以所选学生的服务时间在同一时间段内的概率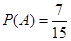 . 13分
. 13分
考点:频率分布直方图,古典概型概率


科目:高中数学 来源: 题型:解答题
李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
| 场次 | 投篮次数 | 命中次数 | 场次 | 投篮次数 | 命中次数 |
| 主场1 | 22 | 12 | 客场1 | 18 | 8 |
| 主场2 | 15 | 12 | 客场2 | 13 | 12 |
| 主场3 | 12 | 8 | 客场3 | 21 | 7 |
| 主场4 | 23 | 8 | 客场4 | 18 | 15 |
| 主场5 | 24 | 20 | 客场5 | 25 | 12 |
 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较 与
与 的大小(只需写出结论)
的大小(只需写出结论)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与
与 ,且乙投球
,且乙投球 次均未命中的概率为
次均未命中的概率为 .
.
(1)求乙投球的命中率 ;
;
(2)若甲投球 次,乙投球
次,乙投球 次,两人共命中的次数记为
次,两人共命中的次数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 | 甲 | | | 乙 | |
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
| 每辆利润(万元) | 1 | 2 | 3 | 1.8 | 2.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1,2,3,4,5名,“二检”中的前5名依然是这五名同学.
(1)求恰好有两名同学排名不变的概率;
(2)如果设同学排名不变的同学人数为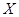 ,求
,求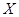 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程 (公里) (公里) | ||
 |  |  | |
| 纯电动乘用车 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |
 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:| 分组 | 频数 | 频率 |
 |  |  |
 |  | 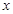 |
 |  |  |
| 合计 |  |  |
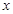 ,
, ,
, ,
, 的值;
的值; 辆纯电动乘用车中任选
辆纯电动乘用车中任选 辆,求选到的
辆,求选到的 辆车续驶里程都不低于
辆车续驶里程都不低于 公里的概率;
公里的概率; 为购买一辆纯电动乘用车获得的补贴,求
为购买一辆纯电动乘用车获得的补贴,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间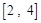 的有8人.
的有8人.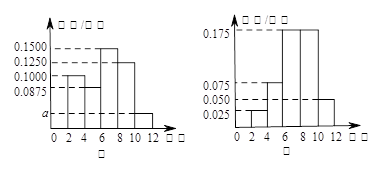
(1)求直方图中 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间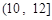 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为 、
、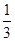 、
、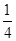 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.
(1)求该参加者有资格闯第三关的概率;
(2)求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com