
已知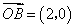 ,
,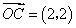 ,
,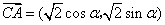 ,则
,则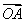 与
与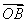 的夹角的取值范围是______________.
的夹角的取值范围是______________.
科目:高中数学 来源: 题型:
全国第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京开幕.期间为了了解国企员工的工资收入状况,从108名相关人员中用分层抽样方法抽取若干人组成调研小组,有关数据见下表:(单位:人)
| 相关人数 | 抽取人数 | |
| 一般职工 | 63 |
|
| 中层 | 27 |
|
| 高管 | 18 | 2 |
(1)求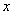 ,
,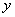 ;
;
(2)若从中层、高管抽取的人员中选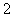 人,求这二人都来自中层的概率.
人,求这二人都来自中层的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
等边三角形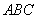 的边长为3,点
的边长为3,点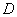 、
、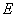 分别是边
分别是边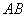 、
、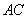 上的点,且满足
上的点,且满足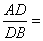
 (如图4).将△
(如图4).将△ 沿
沿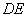 折起到△
折起到△ 的位置,使二面角
的位置,使二面角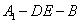 成直二面角,连结
成直二面角,连结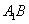 、
、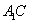
(如图5).
(1)求证: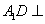 平面
平面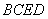 ;
;
(2)在线段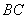 上是否存在点
上是否存在点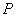 ,使直线
,使直线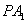 与平面
与平面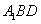 所成的角为
所成的角为 ?若存在,求出
?若存在,求出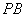 的长,若不存在,请说明理由
的长,若不存在,请说明理由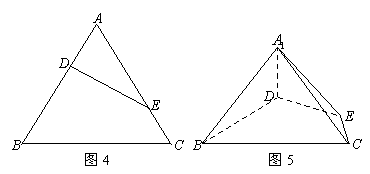 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为 米,高为
米,高为 米,体积为
米,体积为 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000 元(
元( 为圆周率). (Ⅰ)将
为圆周率). (Ⅰ)将 表示成
表示成 的函数
的函数 ,并求该函数的定义域;zhangwlx
,并求该函数的定义域;zhangwlx
(Ⅱ)讨论函数 的单调性,并确定
的单调性,并确定 和
和 为何值时该蓄水池的体积最大.zhang
为何值时该蓄水池的体积最大.zhang
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com