
分析 先求出当p真、q真时,a的取值范围,由p、q一真一假列式计算即可,
解答 解:命题p真:?m∈[-1,1],不等式a2-5a+7≥m+2恒成立⇒a2-5a+7≥(m+2)max=3⇒a≤1或a≥4;
命题q真:x2+ax=2=0有两个不同的实数根⇒△=a2-8>0⇒a<-$2\sqrt{2}$或a$>2\sqrt{2}$;
若p∨q为真,且p∧q为假,则p、q一真一假,
当p真q假时,$\left\{\begin{array}{l}{a≤1或a≥4}\\{-2\sqrt{2}≤a≤2\sqrt{2}}\end{array}\right.$⇒-2$\sqrt{2}$≤a≤1
当p假q真时,$\left\{\begin{array}{l}{1<a<4}\\{a<-2\sqrt{2}或a>2\sqrt{2}}\end{array}\right.$⇒2$\sqrt{2}$<a<4
∴实数a的取值范围为:⇒-2$\sqrt{2}$≤a≤1或2$\sqrt{2}$<a<4.
点评 本题考查了复合命题的真假的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{3}}]$ | B. | $({1,\sqrt{2}}]$ | C. | $[{\sqrt{3},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a≤1或a≥9 | B. | a≤1或a≥9 | C. | 1≤a≤9 | D. | a≥9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
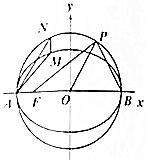 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | b>a>c | C. | b>a>c | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com