
| A. | 4 | B. | 7 | C. | 8 | D. | 9 |
分析 求出函数f(x)的周期,画出函数的图象,函数g(x)=f(x)-|log4|x||的零点个数,转化为:y=f(x)的图象与y=|log4|x||图象交点个数.
解答 解:定义在R上的函数f(x)满足f(4+x)=f(x),函数的周期为4,
且x∈(-2,2]时,f(x)=$\left\{\begin{array}{l}{\frac{1}{2}(|x+\frac{1}{x}|-|x-\frac{1}{x}|),0<x≤2}\\{-({x}^{2}+2x),-2<x≤0}\end{array}\right.$,
函数g(x)=f(x)-|log4|x||的零点个数,就是:y=f(x)的图象与y=|log4|x||图象交点个数.
画出函数的图象如图,y=f(x)∈[0,1],y=|log4|x||是偶函数,当x=4时y=1,|x|>4与y=f(x)
的图象没有交点,由函数的图象可知两个函数的交点个数为9个.(图象中红点).
故选:D.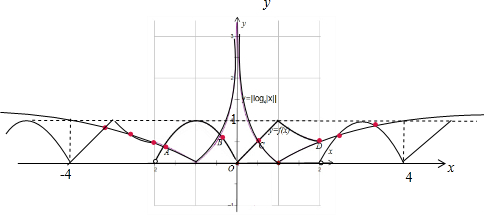
点评 本题考查函数的零点个数的判断,考查数形结合以及分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
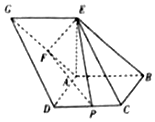 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE查看答案和解析>>
科目:高中数学 来源: 题型:解答题
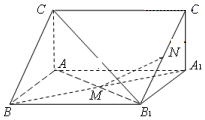 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com