
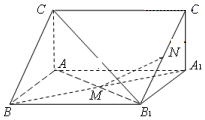
 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点分析 (Ⅰ)设K是B1C的中点,分别在△AB1C,△B1C1C中利用三角形中位线定理可得MK∥AC,KN∥CC1,再由线面平行的判定可得MN∥平面A1ACC1;
(Ⅱ)由已知求得△ABC的面积,然后利用${V}_{{C}_{1}-AB{A}_{1}}=\frac{1}{3}{V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$求得答案.
解答 (Ⅰ)证明:设K是B1C的中点,分别在△AB1C,△B1C1C中利用三角形中位线定理可得:
MK∥AC,KN∥CC1,
又MK∩NK=K,∴平面MNK∥平面AA1C1C,
又MN?平面MNK,∴MN∥平面A1ACC1;
(Ⅱ)解:∵∠CAB=90°,AB=2,BC=$\sqrt{5}$,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}=1$,则S△ABC=1,
∵ABC-A1B1C1是直棱柱,∴高为AA1=2,
∴棱柱ABC-A1B1C1的体积为${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}=2$.
∴${V}_{{C}_{1}-AB{A}_{1}}=\frac{1}{3}{V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}=\frac{2}{3}$.
点评 本题考查线面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 最大值8 | B. | 最小值10 | C. | 最大值12 | D. | 最小值14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$与$\overrightarrow{b}$同向,则$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 当实数λ=0时,λ$\overrightarrow{a}$=0 | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 随m的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a≤1或a≥9 | B. | a≤1或a≥9 | C. | 1≤a≤9 | D. | a≥9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
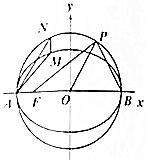 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com