
| A. | 1 | B. | 2 | C. | 3 | D. | 随m的变化而变化 |
分析 先求出P的坐标,得出切线方程,求出三角形F1PF2的内切圆的半径、直线F1M的方程,联立求出N的横坐标,即可得出结论.
解答 解:联立两曲线方程,消去y可得x=$\frac{2}{\sqrt{m}}$,
设P(x0,y0),直线l的方程为$\frac{{x}_{0}x}{4}+\frac{{y}_{0}y}{4-m}$=1①,
设三角形F1PF2的内切圆的半径为r,则由等面积可得$2\sqrt{m}{y}_{0}$=(4+$2\sqrt{m}$)r,
∴r=$\frac{\sqrt{m}{y}_{0}}{2+\sqrt{m}}$=yM②,
直线F1M的方程为y=$\frac{{y}_{M}}{1+\sqrt{m}}$(x+$\sqrt{m}$)③,
联立①②③,化简可得$3\sqrt{m}$x=6$\sqrt{m}$,
∴xN=2,
∵xM=1,
∴xM+xN=3
故选:C.
点评 本题考查题意、双曲线方程的性质,考查直线与椭圆的位置关系,正确计算是关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 7 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
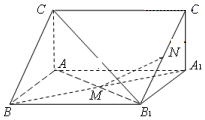 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
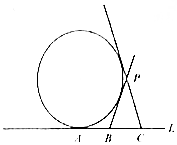 如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)
如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$+1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com