练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a＝(－1，2)，b＝(－1，1)，c＝(3，－2)，用a、b作基底，可将向量c表示为c＝pa＋qb，则

    [　　]

    A．p＝4，q＝1

    B．p＝1，q＝－4

    C．p＝0，q＝4

    D．p＝1，q＝4

    答案：B
    提示：

    由(3，－2)＝p(－1，2)＋q(－1，1)得


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    设A＝3n+Cn13n-1 + Cn23n-2+ … + Cnn-13, 则A的值为

    [　　]

    A. 4n　　B. 4n-1　　C. 3n+1　　D. 4n+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A＝{x||x+1|≤2}，B＝{x|x2－5x+6≥0}，则A、B之间的关系是

    A.AB                                                           B.A＝B

    C.AB                                                          D.A∩B＝

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A＝{x|－1≤x≤2}，B＝{x|x2－(2m＋1)x＋2m<0}.

    (1)当m<时，化简集合B；

    (2)若A∪B＝A，求实数m的取值范围；

    (3)若∩B中只有一个整数，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2014届江西省南昌市高三上学期第一次月考理科数学试卷（解析版） 题型：解答题

    仔细阅读下面问题的解法：

    设A＝[0，1]，若不等式21－x+a>0在A上有解，求实数a的取值范围.

    解：令f(x)＝21－x+a，因为f(x)>0在A上有解。

    ＝2+a>0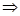a>-2

    学习以上问题的解法，解决下面的问题，已知：函数f(x)=x2+2x+3(-2≤x≤-1).

    ①求f(x)的反函数f-1(x)及反函数的定义域A；

    ②设B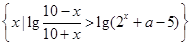＝，若A∩B≠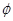,求实数a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省高三元月双周练习数学试卷 题型：填空题

    设集合A＝{x|－1≤x≤2}，B＝{x|0≤x≤4}，则A∪B＝     ▲     ．

     

    查看答案和解析>>

    同步练习册答案