Question

若复数z满足z=i（2+z）（i是虚数单位），则在复平面内z对应的点落在（ ）
A．第一象限
B．第二象限
C．第三象限
D．第四象限

Answer 1

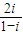
【答案】分析：由复数z满足z=i（2+z），可得z=，利用两个复数代数形式的除法法则化为-1+i，故复数z在复平面内的对应点为（-1，1），从而得到结论．
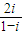
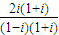
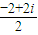
解答：解：∵复数z满足z=i（2+z），∴z====-1+i．
故复数z在复平面内的对应点为（-1，1），
故选：B．
点评：本题主要考查两个复数代数形式的除法，两个复数相除，分子和分母同时乘以分母的共轭复数．还考查复数与复平面内对应点之间的关系，求出z=-1+i，是解题的关键．