考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①利用三角函数的性质即可判断出;
②利用不等式的性质即可判断出;
③利用函数零点的判定定理和函数的单调性即可判断出;
④利用双曲线的定义及其性质即可判断出.
解答:
解:①∵
f(-)=
3sin(-×2-)=-
,因此函数f(x)=3sin(2x-
)的图象关于点(-
,0)不对称,因此不正确;
②若a≥b>-1,则1+a>0,1+b>0,∴a(1+b)-b(1+a)=a-b≥0,∴
≥,因此正确;
③令函数f(x)=x
3+x
2+1,
f′(x)=3x(x+),令f
′(x)=0,解得x=0或
-.当x>0或
x<-时,f
′(x)>0,函数
f(x)单调递增;当
-<x<0时,f
′(x)<0,函数f(x)单调递减.∴当x=0时,函数f(x)取得极小值,
且f(0)=1>0,∴函数在区间
(-,+∞)上无零点,而当x
<-时,f(-2)=(-2)
3+(-2)
2+1=-3<0,f(-1)=1>0,由函数零点的判定定理及其单调性可知:函数f(x)在R上存在唯一零点x
0∈(-2,-1),因此正确.
④由x
2-
=1,可得
c==
.
∴F
1(-,0),F
2(,0),
而|PF
2|=4,∴点P必在双曲线的右支上,
∴|PF
1|=|PF
2|+2a=4+2=6.
因此不正确.
综上可知:只有②③正确.
故答案为:②③.
点评:本题综合考查了三角函数的性质、不等式的性质、函数的单调性及其函数零点的判定定理、双曲线的定义等基础知识,属于基础题.



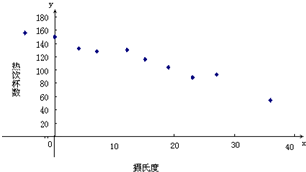 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
 椭圆C:
椭圆C: