
 4,BC = 3,沿对角线AC把矩形折成二面角D-AC-B,并且
4,BC = 3,沿对角线AC把矩形折成二面角D-AC-B,并且 D点在平面ABC内的射影落在AB上.若在四面体D-
D点在平面ABC内的射影落在AB上.若在四面体D- ABC内有一球,当球的体积最大时,球的半径是 .
ABC内有一球,当球的体积最大时,球的半径是 . C, 又∵BD
C, 又∵BD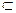 平面DBC,∴AD⊥BD,∴△ABD为直角三角形,∵AB = 4,AD = 3,∴BD = ,∴S△ABC = AD·BD = ×3×= .在△DAB和△DBC中,∵AD = BC,AB = DC,DB = DB,∴△DAB
平面DBC,∴AD⊥BD,∴△ABD为直角三角形,∵AB = 4,AD = 3,∴BD = ,∴S△ABC = AD·BD = ×3×= .在△DAB和△DBC中,∵AD = BC,AB = DC,DB = DB,∴△DAB ≌△BCD,故S△DBC = ,VD -ABC =" VA" –DBC = ×3×= ,∴S△ABC = S△ADC = 6,∴R(6 + 6 +
≌△BCD,故S△DBC = ,VD -ABC =" VA" –DBC = ×3×= ,∴S△ABC = S△ADC = 6,∴R(6 + 6 + + ),于是( 4 + )R =
+ ),于是( 4 + )R =  , 解得R =
, 解得R = 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com