
 中,二面角
中,二面角 的平面角等于 ( )
的平面角等于 ( ) B.
B. C .
C . D
D 
 的棱长为1,以DA为x轴,以DC为y轴,以DD
的棱长为1,以DA为x轴,以DC为y轴,以DD 为z轴,建立空间直角坐标系,则
为z轴,建立空间直角坐标系,则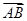 =(0,1,0),
=(0,1,0),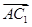 =(-1,1,1),求出设面ABC
=(-1,1,1),求出设面ABC 的法向量
的法向量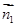 =(1,0,1),面ABC的法向量
=(1,0,1),面ABC的法向量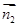 =(0,0,1),由向量法能求出二面角C1-AB-C的平面角.
=(0,0,1),由向量法能求出二面角C1-AB-C的平面角.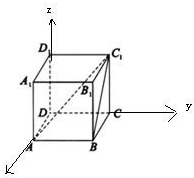
 的棱长为1,
的棱长为1, 为z轴,建立空间直角坐标系,
为z轴,建立空间直角坐标系,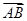 =(0,1,0),
=(0,1,0),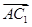 =(-1,1,1),
=(-1,1,1),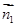 =(x,y,z),
=(x,y,z),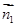 ?
?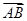 =0,
=0,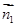 ?
?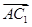 =0,
=0, ,∴
,∴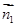 =(1,0,1),
=(1,0,1),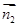 =(0,0,1),
=(0,0,1),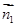 ,
,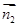 >|
>|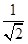 |=|
|=|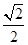 ,
,

科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
|
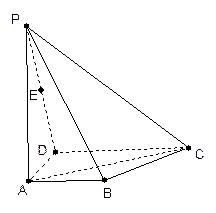
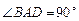 ,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.8 | B.4 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 4,BC = 3,沿对角线AC把矩形折成二面角D-AC-B,并且
4,BC = 3,沿对角线AC把矩形折成二面角D-AC-B,并且 D点在平面ABC内的射影落在AB上.若在四面体D-
D点在平面ABC内的射影落在AB上.若在四面体D- ABC内有一球,当球的体积最大时,球的半径是 .
ABC内有一球,当球的体积最大时,球的半径是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com