Question

二阶矩阵A，B对应的变换对圆的区域作用结果如图所示.

（1）请写出一个满足条件的矩阵A，B；
（2）利用（1）的结果，计算C=BA，并求出曲线在矩阵C对应的变换作用下的曲线方程.

Answer 1

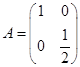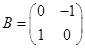（1）， ；（2）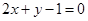

解析试题分析：（1）由图形的变化可知二阶矩阵A对应的变换是横坐标不变，纵坐标变为原来一半的变换，由此可得矩阵A.矩阵B对应的变换是逆时针旋转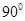的旋转变换，由此可得矩阵B.
（2）由（1）的结果，可得C=BA，要求出曲线在矩阵C对应的变换作用下的曲线方程.只需要在曲线上任取一点，求出该点在矩阵C作用对应的点，再代入已知的曲线方程即可得到结论.
（1）由题意，二阶矩阵A对应的变换是横坐标不变，纵坐标变为原来一半的变换，故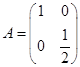
二阶矩阵B对应的变换是逆时针旋转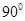的旋转变换，故 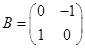     4分
（2）C=BA=，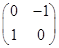
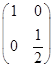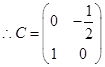
设曲线上任意一点为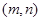，变换后的点坐标为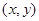
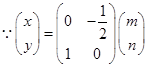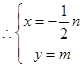，，故所求的曲线方程为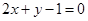                           7分
考点：1.图形表示矩阵的变换.2.矩阵的运算.