
| A. | ?x∈R,都有$x_{\;}^2+2x+5≠0$ | B. | ?x∈R,都有$x_{\;}^2+2x+5=0$ | ||
| C. | ?x0∈R,都有$x_0^2+2{x_0}+5≠0$ | D. | ?x∉R,都有$x_{\;}^2+2x+5≠0$ |
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
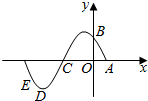 已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )
已知A,B,C,D是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)一个周期内的图象上的四个点,如图所示,$A(\frac{π}{6},0)$,B为y轴上的点,D为图象上的最低点,C为该函数图象的一个对称中心,B与E关于点C对称,$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$,则$f(-\frac{π}{6})$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 加油类型 汽车排量 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com