
【题目】某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为![]() 、
、![]() 、
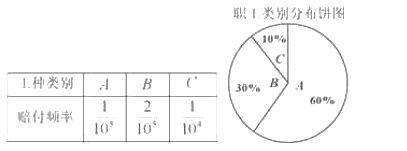
、![]() 三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
对于![]() 、
、![]() 、
、![]() 三类工种职工每人每年保费分别为
三类工种职工每人每年保费分别为![]() 元,
元,![]() 元,
元,![]() 元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费![]() 、
、![]() 所要满足的条件;
所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业于保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择翻翻2的支出(不包括职工支出)低于选择方案1的支出期望,求保费![]() 、
、![]() 所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
【答案】(Ⅰ)![]() 元;(Ⅱ)企业有可能与保险公司合作.
元;(Ⅱ)企业有可能与保险公司合作.
【解析】试题分析:(1)分别求出工种![]() 、工种
、工种![]() 、工种C赔偿金额的期望,根据保险公司要求利润的期望不低于保费的20%可得结果;(2)求出该企业不与保险公司合作赔偿金的期望值及该企业与保险公司合作保费支出,比较大小即可得结果.
、工种C赔偿金额的期望,根据保险公司要求利润的期望不低于保费的20%可得结果;(2)求出该企业不与保险公司合作赔偿金的期望值及该企业与保险公司合作保费支出,比较大小即可得结果.
试题解析:(Ⅰ)设工种![]() ,
,![]() ,
,![]() 职工的每份保单保险公司的效益为随机变量
职工的每份保单保险公司的效益为随机变量![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
保险公司期望收益![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
根据要求
![]()
![]()
![]()
![]()
![]()
![]() .
.
解得![]() ,
,
所以每张保单的保费需要满足![]() 元.
元.
(Ⅱ)若该企业不与保险公司合作,则安全支出,即赔偿金的期望值为
![]()
![]()
![]() .
.
若该企业与保险公司合作,则安全支出,即保费为
![]()
![]() .
.
解得![]() ,
,
结果与(Ⅰ)不冲突,所以企业有可能与保险公司合作.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】有能力互异的3人应聘同一公司,他们按照报名顺序依次接受面试,经理决定“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”,记该公司录用到能力最强的人的概率为p,录用到能力中等的人的概率为q,则(p,q)=( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业招聘会的现场,所有应聘者的初次面试都由张、王、李三位专家投票决定是否进入下一轮测试,张、王、李三位专家都有“通过”、“待定”、“淘汰”三类票各一张,每个应聘者面试时,张、王、李三位专家必须且只能投一张票,每人投三类票中的任意一类的概率均为 ![]() ,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
,且三人投票相互没有影响,若投票结果中至少有两张“通过”票,则该应聘者初次面试获得“通过”,否则该应聘者不能获得“通过”.
(1)求应聘者甲的投票结果获得“通过”的概率;
(2)记应聘者乙的投票结果所含“通过”和“待定”票的票数之和为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)经过原点作直线![]() (不与坐标轴重合)交椭圆于
(不与坐标轴重合)交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 轴于点
轴于点![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线..
三点共线..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,线段
上的一个动点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 相交于点
相交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)记点![]() 的轨迹为
的轨迹为![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的两点,满足
上的两点,满足![]() ,曲线
,曲线![]() 的过
的过![]() ,
,![]() 的两条切线(异于
的两条切线(异于![]() )交于点
)交于点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() 以极点为平面直角坐标系的原点,极轴为
以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )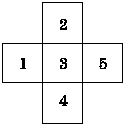
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com