
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() 以极点为平面直角坐标系的原点,极轴为
以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点所在直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
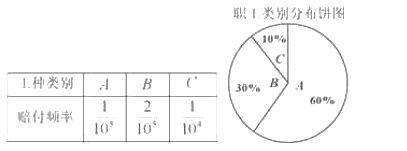
对于![]() 、
、![]() 、
、![]() 三类工种职工每人每年保费分别为
三类工种职工每人每年保费分别为![]() 元,
元,![]() 元,
元,![]() 元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费![]() 、
、![]() 所要满足的条件;
所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业于保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择翻翻2的支出(不包括职工支出)低于选择方案1的支出期望,求保费![]() 、
、![]() 所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
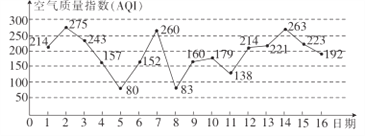
(1)若该人到达后停留![]() 天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
(2)若该人到达后停留3天(到达当日算1天〉,设![]() 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
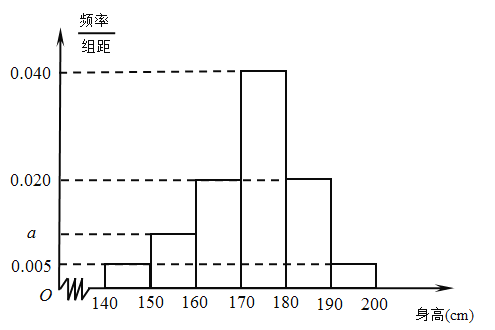
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取![]() 人,用
人,用![]() 表示身高在
表示身高在![]() 以上的男生人数,求随机变量
以上的男生人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com