练习册

  • 练习册
  • 试题
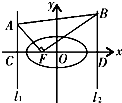
    精英家教网 > 高中数学 > 题目详情

    如图，已知F(0，1)，直线l∶y=－2，圆C∶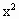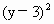＋=1

    　　

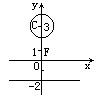
    (Ⅰ)右动点M到点F的距离比它到直线l的距离小1，求动点M轨迹E的方程；

    (Ⅱ)过E上一点P作圆C的切线，切点为A、B，问四边形PACB的面积S有没有最小值？如果有，求出S的最小值和S取最小值时P点的坐标；如果没有，说明理由．

    答案：
    解析：

    　　解：(Ⅰ)方法一：

    　　设动点M(x，y)．由题设条件可知

    　　

    　　①当y＋2≥0时，即y≥－2时，有=(y＋2)－1 两端平方并整理得

    　　②当y＋2＜0即y＜－2时有=－(y＋2)－1 两端平方并整理得

    　　这与y＜－2矛盾．(注：若由图象观察说明此种情况不可能，则不扣分)综合①②知轨迹E的方程为

    　　方法二：

    　　显然，在x轴下方不存在满足条件的点M，所以题中条件等价于：

    　　“动点M到点F的距离和它到直线y=－1的距离相等．”

    　　根据抛物线的定义，M点的轨迹是以点F(0，1)为焦点，直线y=－1为准线的抛物线．

    　　所以轨迹E的方程是

    　　(Ⅱ)连PC，不难发现

    　　∵ CA⊥PA且|AC|=1 ∴S=2··|AP|·|AC|

    　　即S=|AP|

    　　设于是，

    　　

    　　∴

    　　当且仅当时“=”成立，此时

    　　所以四边形PACB存在最小值，最小值是，此时P点坐标是(±2，1)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，已知椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左、右准线分别为l1，l2，且分别交x轴于C，D两点，从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与交于点B，若AF⊥BF，且∠ABD=75°，则椭圆的离心率等于
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

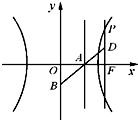    精英家教网如图，已知双曲线
    x2
    a2
    -
    y2
    b2
    =1 (a＞0，b＞0)    的右准线交x轴于A，虚轴的下端点为B，过双曲线的右焦点F（c，0）作垂直于x轴的直线交双曲线于P，过点A、B的直线与FP相交于点D，且2
    OD
    =
    OF
    +
    OP
    （O为坐标原点）．
    （Ⅰ）求双曲线的离心率；
    （Ⅱ）若a=2，过点（0，-2）的直线l交该双曲线于不同两点M、N，求
    OM
    •
    ON
    的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    1
    x2+1
    ，令g（x）=f（
    1
    x
    ）．
    （1）求函数f（x）的值域；
    （2）求证：f（x）+g（x）=1（x≠0）；
    （3）如图，已知f（x）在区间[0，+∞）的图象，请据此在该坐标系中补全函数f（x）在定义域内的图象，并在同一坐标系中作出函数g（x）的图象．请说明你的作图依据．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，已知椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左、右准线分别为l1、l2，且分 别交x轴于C、D两点，从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B，若AF⊥BF且∠CAB=105°，则椭圆的离心率等于（　　）
    A、
    		6
    -
    		2
    2
    B、
    		3
    -1
    C、
    		6
    -
    		2
    4
    D、
    		3
    -1
    2

    查看答案和解析>>

    同步练习册答案