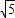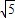【答案】
分析:(1)由题意得直线l
1的方程和过原点垂直于l
1的直线方程,两个方程联立求得交点的横坐标,根据椭圆中心O(0,0)关于直线l
1的对称点在直线x=
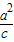
上,进而求得a和c的关系,进而根据直线l
1求得椭圆的焦点,求得c,则a和b可求得,进而得到椭圆的方程.
(2)当直线l
1的斜率存在时,设直线l
1的方程代入椭圆方程,设M(x
1,y
1),N(x
2,y
2)利用韦达定理表示出x
1+x
2和x
1x
2,进而表示出|MN|,进而利用点到直线的距离求得坐标原点O到直线l
2的距离根据(
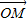
•
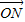
)•sin∠MON=
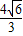
求得三角形MON的面积,把|MN|和d代入求得k;当直线l
2的斜率不存在时,直线l
2的方程为x=-2,综合答案可得.
解答:解(Ⅰ)由题意得直线l
1的方程为y=
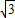
x-2
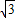
,①
过原点垂直于l
1的直线方程为y=-
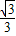
x②
解①②得:x=

因为椭圆中心O(0,0)关于直线l
1的对称点在直线x=
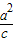
上,
∴
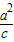
=3
又∵直线l
1过椭圆焦点,∴该焦点坐标为(2,0),
∴c=2,a
2=6,b
2=2
故椭圆C的方程为
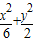
=1③
(II)当直线l
1的斜率存在时,
设直线l
1的方程为y=k(x+2),代入③并整理得:
(3k
2+1)x
2+12k
2x+12k
2-6=0
设M(x
1,y
1),N(x
2,y
2)
则x
1+x
2=-
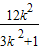
,x
1x
2=
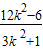
∴|MN|=
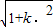
|x
1-x
2|=
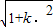
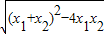
=
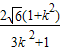
坐标原点O到直线l
2的距离d=
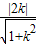
.
∵(
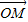
•
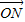
)•sin∠MON=
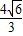
,即S
△MON=
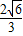
而S
△MON=

||MN|d
∴|NM|d=
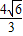
,即
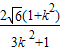
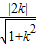
=
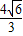
解得k=±
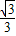
,此时直线l
2的方程为y=±
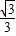
(x+2)
当直线l
2的斜率不存在时,直线l
2的方程为x=-2
此时点M(-2,
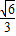
),N(-2,-
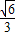
),满足S
△MON=
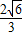
,
综上得,直线l
2的方程为x=-2或±
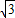
y+2=0.
点评:本题主要考查了直线与圆锥曲线的综合问题.在设直线方程的时候,一定要考虑斜率不存在时的情况,以免答案不全面.

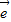 =(1,
=(1,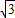 )平行的直线l1过点A(0,-2
)平行的直线l1过点A(0,-2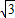 ),椭圆C:
),椭圆C: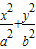 =1(a>b>0)的中心关于直线l1的对称点在直线x=
=1(a>b>0)的中心关于直线l1的对称点在直线x=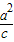 (c2=a2-b2)上,且直线l1过椭圆C的焦点.
(c2=a2-b2)上,且直线l1过椭圆C的焦点.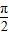 ,且•sin∠MON=
,且•sin∠MON=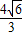 ,(O为坐标原点),求直线l12的方程.
,(O为坐标原点),求直线l12的方程.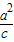 上,进而求得a和c的关系,进而根据直线l1求得椭圆的焦点,求得c,则a和b可求得,进而得到椭圆的方程.
上,进而求得a和c的关系,进而根据直线l1求得椭圆的焦点,求得c,则a和b可求得,进而得到椭圆的方程.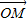 •
•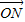 )•sin∠MON=
)•sin∠MON=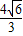 求得三角形MON的面积,把|MN|和d代入求得k;当直线l2的斜率不存在时,直线l2的方程为x=-2,综合答案可得.
求得三角形MON的面积,把|MN|和d代入求得k;当直线l2的斜率不存在时,直线l2的方程为x=-2,综合答案可得.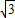 x-2
x-2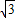 ,①
,①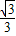 x②
x②
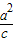 上,
上,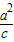 =3
=3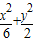 =1③
=1③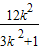 ,x1x2=
,x1x2=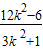
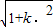 |x1-x2|=
|x1-x2|=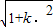
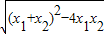 =
=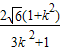
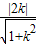 .
.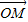 •
•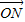 )•sin∠MON=
)•sin∠MON=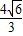 ,即S△MON=
,即S△MON=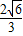
 ||MN|d
||MN|d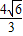 ,即
,即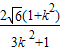
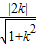 =
=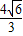
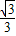 ,此时直线l2的方程为y=±
,此时直线l2的方程为y=±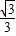 (x+2)
(x+2)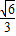 ),N(-2,-
),N(-2,-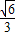 ),满足S△MON=
),满足S△MON=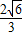 ,
,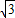 y+2=0.
y+2=0.

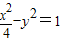 相交于A、B两点,则|AB|的最小值为( )
相交于A、B两点,则|AB|的最小值为( )