
【题目】已知关于x的不等ax2﹣3x+2>0的解集{x|x<1或x>b}
(Ⅰ)求a,b的值;
(Ⅱ)解关于x的不等式:ax2﹣(ac+b)x+bx<0.
【答案】解:(Ⅰ)∵不等式ax2﹣3x+2>0的解集是{x|x<1或x>b},
∴方程ax2﹣3x+2=0的实数根是1和b,
由根与系数的关系,得;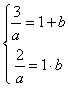
解得a=1,b=2;
(Ⅱ)∵a=1,b=2;
∴不等式ax2﹣(ac+b)x+bx<0化为
x2﹣(c+2)x+2x<0,
即x(x﹣c)<0;
∴当c>0时,解得0<x<c,
当c=0时,不等式无解,
当c<0时,解得c<x<0;
综上,当c>0时,不等式的解集是(0,c),
当c=0时,不等式的解集是,
当c<0时,不等式的解集是(c,0).
【解析】(Ⅰ)根据不等式ax2﹣3x+2>0的解集,得出方程ax2﹣3x+2=0的实数根,由根与系数的关系,求出a、b的值;(Ⅱ)由a、b的值,化简不等式ax2﹣(ac+b)x+bx<0,讨论c的值,求出不等式的解集即可.
【考点精析】认真审题,首先需要了解解一元二次不等式(求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知在直角坐标![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为:
的参数方程为: 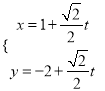 ,曲线
,曲线![]() 的极坐标方程:
的极坐标方程: ![]()
(1)写出![]() 和
和![]() 的普通方程;
的普通方程;
(2)若![]() 与
与![]() 交于两点
交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一元二次不等式﹣x2+x+2>0的解集是( )
A.{x|x<﹣1或x>2}
B.{x|x<﹣2或x>1}
C.{x|﹣1<x<2}
D.{x|﹣2<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)证明:数列{ ![]() }是等比数列;
}是等比数列;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com