
����Ŀ�����������С�������������Ͷ�����ҹ�����Ѹ�ͷ�չ��������������Ϊ���dz����ṩ�˺ܴ�ı�������Ҳ�����еĹ���������һЩ���ѣ���ij����Ϊ�˽����Ƕԡ�����������Ͷ�ŵ��Ͽɶȣ���![]() ����ε���Ⱥ�����ȡ
����ε���Ⱥ�����ȡ![]() �˽�����һ�Ρ����Ƿ���Ͷ�Ź������������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ�Ρ����Ƿ���Ͷ�Ź������������ʾ����飬���ݵ������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
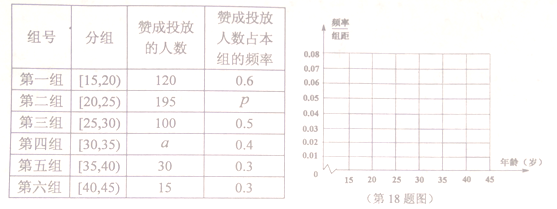
��1����ȫƵ�ʷֲ�ֱ��ͼ������![]() ��ֵ��
��ֵ��
��2���ڵ��ġ��塢���顰��Ͷ�Ź��������������У��÷ֲ�����ķ�����ȡ7�˲μӡ������������ﳵ����������ġ��塢����Ӧ�ֱ��ȡ��������
��3���ڣ�2���г�ȡ��7�������ѡ��2����Ϊ�����ӳ�������ѡ�ɵ�2��û�е������˵ĸ���.
���𰸡���1������������2��4�ˣ�2�ˣ�1������3��![]()
�������������������1����Ƶ�ʱ��е��������ݿ�֪��������������Ϊ100�����Ƶ�ʷֲ�ֱ��ͼ�ɵ�![]() ��
��![]() �����ݵڶ������
�����ݵڶ������![]() ����2�����ݷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ������Ϊ4�ˣ�2�ˣ�1�ˣ���3�������оٷ��г���7���������ȡ2��������п��ܵĽ����21�֣�����ǡ��û�е������˵����п��ܽ��4�֣��ʿɵý��.
����2�����ݷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ������Ϊ4�ˣ�2�ˣ�1�ˣ���3�������оٷ��г���7���������ȡ2��������п��ܵĽ����21�֣�����ǡ��û�е������˵����п��ܽ��4�֣��ʿɵý��.
�����������1����ͼ������ͼ����Ƶ�ʱ��е��������ݿ�֪��������������Ϊ![]() ���ٽ��Ƶ�ʷֲ�ֱ��ͼ
���ٽ��Ƶ�ʷֲ�ֱ��ͼ

��֪![]() ������
������![]() ���ڶ����Ƶ��Ϊ
���ڶ����Ƶ��Ϊ![]() ������
������![]()
��2����Ϊ���ġ��塢���顰ϲ���ﳵ������������105�ˣ��ɷֲ����ԭ����֪�����ġ��塢����ֱ�ȡ������Ϊ4�ˣ�2�ˣ�1��.
��3���������4����![]() ��������2����
��������2����![]() ��������1����
��������1��Ϊ��![]() .���7���������ȡ2��������п��ܵĽ��Ϊ��
.���7���������ȡ2��������п��ܵĽ��Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��21�֣� ����ǡ��û�е������˵����п��ܽ��Ϊ��
��21�֣� ����ǡ��û�е������˵����п��ܽ��Ϊ��![]() ����3�֣���������ȡ��2����ǡ��û�е������˵ĸ���Ϊ
����3�֣���������ȡ��2����ǡ��û�е������˵ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�ֵ��⣬���ֵ���ı����ں̣ܶ����뵱���������������ױ��ʣ��õ����ÿ����ÿ��16Ԫ�ijɱ��۸��������ֵ������ɿ飬Ȼ����ÿ��26Ԫ�ļ۸���ۣ�������������꣬ʣ�µĵ���ֻ����ÿ��6Ԫ�ͼ۳��ۣ�������¼��100����ֵ������������n����λ���飬n��N*����������ͼ�� 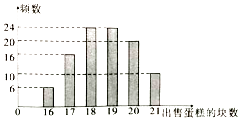
��1�����õ����ijһ������19�鵰�⣬���������y����λ��Ԫ�����ڵ���������n�ĺ�������ʽ��
��2����Ҫ����ۡ����۵ĵ��������С��n����Ƶ�ʲ�С��0.4����n�����ֵ��
��3�����õ������100��ÿ�춼����19�鵰�⣬�Լ�����100�쵰������������ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x���Ƕ�����[��4��4]�ϵ�ż��������f��x��= ![]() ����ʽ��1��2x��g��log2x����0�Ľ⼯�������ʾΪ
����ʽ��1��2x��g��log2x����0�Ľ⼯�������ʾΪ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ��ΪR������f��x��= ![]() �Ķ�����ΪM����RM=�� ��
�Ķ�����ΪM����RM=�� ��
A.�����ޣ���1��
B.[1��+�ޣ�
C.��1��+�ޣ�
D.�����ޣ�1]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������� p(n) �� n=k ��������ô���� n=k+2 Ҳ���������� p(n) �� n=2 �����������н�����ȷ���ǣ� ��
A.p(n) ��������Ȼ�� n ����
B.p(n) ��������ż�� n ����
C.p(n) ������������ n ����
D.p(n) �����д���1����Ȼ�� n ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������{an} ��ǰ n ��ĺͼ�Ϊ Sn .S
������{an} ��ǰ n ��ĺͼ�Ϊ Sn .S
��1����S1,S2,S3��ֵ������Sn�ı���ʽ��
��2��������ѧ���ɷ�֤����IJ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() .
.
��1��������ʽ![]() �����,�� a ��ȡֵ��Χ;
�����,�� a ��ȡֵ��Χ;
��2���� a=2 ʱ,����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=f��x���Ƕ�����a��b�ϵ�������������a��b��R��0��b����a����֪y=f��x������㣬�躯��F��x��=f2��x��+f2����x���������F��x���������ĸ�˵����
�ٶ�������[��b��b]������ż����������Сֵ��0�����ڶ������ڵ���������
������ȷ��������������Ϊ��ȷ��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������
������![]() ��
�� ![]() ���ĸ����㹹�ɵ��ı������Ϊ
���ĸ����㹹�ɵ��ı������Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������Բ![]() ���Ƿ������������
���Ƿ������������![]() ��ʹ������:��ֱ��
��ʹ������:��ֱ��![]() ��ֱ��
��ֱ��![]() ��б�ʻ�Ϊ�෴�������߶�
��б�ʻ�Ϊ�෴�������߶�![]() ���е���
���е���![]() ���ϣ������ڣ����
���ϣ������ڣ����![]() ��ƽ��������Բ�ཻ�����ҵ��ҳ����������ڣ���˵������.
��ƽ��������Բ�ཻ�����ҵ��ҳ����������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com