
(2)若函数f(x)=sin(x+φ)为偶函数,求φ的值.
解析:(1)函数f(x)=|sinx|+cosx的定义域是R,
∵f(-x)=|sin(-x)|+cos(-x)=|-sinx|+cosx=|sinx|+cosx=f(x),
∴f(x)是偶函数.
(2)∵f(x)=sin(x+φ)是偶函数,
∴f(-x)=f(x),即
sin(-x+φ)=sin(x+φ)(x∈R).
∴sin(x+φ)+sin(x-φ)=0(x∈R).
∴2sinxcosφ=0(x∈R).
∵当x∈R时,sinx不恒为零,
∴cosφ=0,φ=kπ+![]() (k∈Z).
(k∈Z).
点评:判断函数奇偶性,首先判断其定义域是否在x轴上关于原点对称,然后判断f(-x)与±f(x)的关系.注意理解f(x)为偶函数的充要条件是f(-x)=f(x)对其定义域内一切x恒成立的含义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)判断函数f(x)=![]() +
+![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(Ⅱ)集合M中的元素f(x)具有下面的性质:若f(x)的定义域为D,则对于任意[m,n]![]() D,都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立,试用这一性质证明:方程f(x)-x=0只有一个实数根;
D,都存在x0∈[m,n],使得等式f(n)-f(m)=(n-m)f′(x0)成立,试用这一性质证明:方程f(x)-x=0只有一个实数根;
(Ⅲ)设x1是方程f(x)-x=0的实数根,求证:对于f(x)定义域中任意的x2,x3,当|x2-x1|<1,且|x3-x1|<1时,|f(x3)-f(x2)|<2.
查看答案和解析>>
科目:高中数学 来源:2014届河北省唐山市高一年级第二学期期末数学试卷 题型:解答题
设函数f (x)=loga(ax+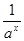 ).(1)判断函数f (x)的奇偶性;
).(1)判断函数f (x)的奇偶性;
(2)判断函数f (x)在(0,+∞)的单调性并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com