②④⑤
分析:根据数列的规律,分母为n时,所对应的项数是(n-1)项.从分母是2开始到分母为n结束共有

项
①前23项构成的数列是:

,

,

,

,

,

,

,

,

,

,

…

,则第23项一目了然.
②易知:前11项构成的数列是:

,

,

,

,

,

,

,

,

,

,

,再求和便知正误.
③数列a
1,a
2+a
3,a
4+a
5+a
6,a
7+a
8+a
9+a
10,…实际上是

,1,

,2,…

,再由数列定义判断
④数列a
1,a
2+a
3,a
4+a
5+a
6,a
7+a
8+a
9+a
10,…实际上是

,1,

,2,…

,先判断数列类型,再用求其前n项和.
⑤通过④的前n项和解不等式,确定k的值,从而再判断终止的项.
解答:①前23项构成的数列是:

,

,

,

,

,

,

,

,

,

,

…

∴

,故不正确;
②由数列可知:前11项构成的数列是:

,

,

,

,

,

,

,

,

,

,

∴s
11=

+

+

+

+

+

+

+

+

+

+

=

,故正确;
③数列a
1,a
2+a
3,a
4+a
5+a
6,a
7+a
8+a
9+a
10,…是

,1,

,2,

由等差数列定义

(常数),所以是等差数列,故不正确.
④∵数列a
1,a
2+a
3,a
4+a
5+a
6,a
7+a
8+a
9+a
10,…是

,1,

,2,…

.
由③知是等差数列,所以由等差数列前n项和公式可知:
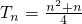
,故正确;
⑤由④知数列a
1,a
2+a
3,a
4+a
5+a
6,a
7+a
8+a
9+a
10,a
11+a
12+a
13+a
14+a
15,a
16+a
17+a
18+a
19+a
20+a
21,是

,1,

,2,

,

+

+…+

∴T
5=7.5<10,T
6=10.5>10,∴
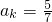
,正确.
故答案为:②④⑤
点评:本题主要考查探究数列的规律,转化数列,构造数列来研究相应数列通项和前n项和问题,这种题难度较大,必须从具体到一般地静心研究,再推广到一般得到结论.

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…,
,…, ,
, ,…,
,…, ,…有如下运算和结论:
,…有如下运算和结论: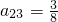 ;
;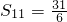
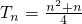 ;
;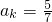 .
. 项
项 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, …
… ,则第23项一目了然.
,则第23项一目了然. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,再求和便知正误.
,再求和便知正误. ,1,
,1, ,2,…
,2,… ,再由数列定义判断
,再由数列定义判断 ,1,
,1, ,2,…
,2,… ,先判断数列类型,再用求其前n项和.
,先判断数列类型,再用求其前n项和. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, …
…
 ,故不正确;
,故不正确; ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ +
+ =
= ,故正确;
,故正确; ,1,
,1, ,2,
,2,
 (常数),所以是等差数列,故不正确.
(常数),所以是等差数列,故不正确. ,1,
,1, ,2,…
,2,… .
.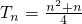 ,故正确;
,故正确; ,1,
,1, ,2,
,2,
 +
+ +…+
+…+
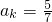 ,正确.
,正确.
