求证:以A(-4,-1,-9),B(-10,1,-6),C(-2,-4,-3)为顶点的三角形是等腰直角三角形.
【答案】
分析:先利用空间两点的距离公式分别求出AB,AC,BC的长,然后利用勾股定理进行判定是否为直角三角形,以及长度是否有相等,从而判定是否是等腰直角三角形.
解答:证明:
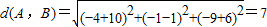
,
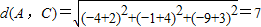
,
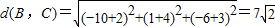
,
∵d
2(A,B)+d
2(A,C)=d
2(B,C)且d(A,B)=d(A,C).
∴△ABC为等腰直角三角形.
点评:本题主要考查了两点的距离公式和勾股定理的应用,考查空间想象能力、运算能力和推理论证能力,属于基础题.
