Question

关于x的方程3x²-6（m-1）x+m²+1=0的两实根为x₁、x₂，若|x₁|+|x₂|=2，求m的值．

Answer 1

解：x₁、x₂为方程两实根，
∴△=36（m-1）²-12（m²+1）≥0．
∴m≥或m≤．
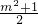
又∵x₁•x₂=＞0，∴x₁、x₂同号．
∴|x₁|+|x₂|=|x₁+x₂|=2|m-1|．
于是有2|m-1|=2，∴m=0或2．
∴m=0．
分析：方程3x²-6（m-1）x+m²+1=0的两实根为x₁、x₂，用△求出m的范围，
结合韦达定理，判定两个根的符号，以及|x₁|+|x₂|=2，可求m 的值．
点评：本题考查一元二次方程根的分布与系数的关系，注意判别式的应用，是基础题．