
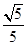 ,sinβ=
,sinβ=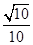 ,且α、β均为锐角,求α+β的值.
,且α、β均为锐角,求α+β的值.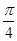
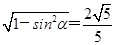 .
.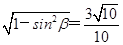 .
.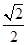 ,
,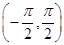 ,则一般选正弦函数.
,则一般选正弦函数.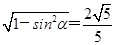 .(2分)
.(2分)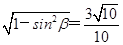 .(4分)
.(4分)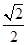 ,(10分)
,(10分)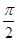 ,0<β<
,0<β<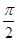 ,所以0<α+β<π,
,所以0<α+β<π,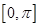 上是单调递减函数,故α+β=
上是单调递减函数,故α+β=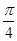 .(14分)
.(14分)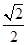 ,0°<α+β<180°而得到α+β=45°或135°是正确的,但题设中sinα=
,0°<α+β<180°而得到α+β=45°或135°是正确的,但题设中sinα=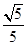 <
<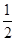 ,sinβ=
,sinβ=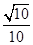 <
<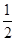 ,使得0°<α<30°,0°<β<30°从而0°<α+β<60°,故上述结论是错误的.在已知值求角中,应合理选择三角函数形式进行求解,避免增根.本题中0<α+β<π,因为y=cosx在
,使得0°<α<30°,0°<β<30°从而0°<α+β<60°,故上述结论是错误的.在已知值求角中,应合理选择三角函数形式进行求解,避免增根.本题中0<α+β<π,因为y=cosx在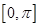 上是单调函数,所以本题先求cos(α+β)不易出错.
上是单调函数,所以本题先求cos(α+β)不易出错.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com