
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 在点
在点![]() 处切线
处切线![]() 的方程;
的方程;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)记![]() ,求证:
,求证: ![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于两个定义域相同的函数f(x),g(x),若存在实数m、n使h(x)=mf(x)+ng(x),则称函数h(x)是由“基函数f(x),g(x)”生成的.
(1)若f(x)=x2+3x和个g(x)=3x+4生成一个偶函数h(x),求h(2)的值;
(2)若h(x)=2x2+3x﹣1由函数f(x)=x2+ax,g(x)=x+b(a、b∈R且ab≠0)生成,求a+2b的取值范围;
(3)利用“基函数f(x)=log4(4x+1),g(x)=x﹣1”生成一个函数h(x),使之满足下列件:①是偶函数;②有最小值1;求函数h(x)的解析式并进一步研究该函数的单调性(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且 ![]() ,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是
,∠AOQ=α,α∈[0,π). (Ⅰ)若点Q的坐标是 ![]() ,求
,求 ![]() 的值;
的值;
(Ⅱ)设函数 ![]() ,求f(α)的值域.
,求f(α)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y. 
(1)求出y关于x的函数f(x)的解析式;
(2)求y的最大值,并指出相应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC= ![]() BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点.
BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点. 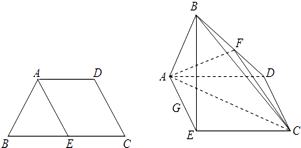
(1)求三棱锥E﹣ACB1的体积;
(2)证明:B1E∥平面ACF;
(3)证明:平面B1GD⊥平面B1DC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() 在R上是奇函数.
在R上是奇函数.
(1)求a;
(2)对x∈(0,1],不等式sf(x)≥2x﹣1恒成立,求实数s的取值范围;
(3)令g(x)= ![]() ,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的个数是( )
①命题“![]() ”的否定为“
”的否定为“![]() ”;
”;
②命题“在![]() 中,
中, ![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
③设![]() 是公比为
是公比为![]() 的等比数列,则“
的等比数列,则“![]() ”是“
”是“![]() 为递增数列”的充分必要条件;
为递增数列”的充分必要条件;
④若统计数据![]() 的方差为
的方差为![]() ,则
,则![]() 的方差为
的方差为![]() ;
;
⑤若两个随机变量的线性相关性越强,则相关系数绝对值越接近1.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com