
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由向量的数量积运算可化问题为二次函数恒成立问题,由二次函数的性质可得.
解答 解:设单位向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$的夹角为θ,
∵对于任意实数λ都有|$\overrightarrow{e_1}$+$\frac{1}{2}$$\overrightarrow{e_2}$|≤|$\overrightarrow{e_1}$-λ$\overrightarrow{e_2}$|成立,
∴对于任意实数λ都有|$\overrightarrow{e_1}$+$\frac{1}{2}$$\overrightarrow{e_2}$|2≤|$\overrightarrow{e_1}$-λ$\overrightarrow{e_2}$|2成立,
即${\overrightarrow{{e}_{1}}}^{2}$+$\frac{1}{4}$${\overrightarrow{{e}_{2}}}^{2}$+|$\overrightarrow{{e}_{1}}$||$\overrightarrow{{e}_{2}}$|cosθ≤${\overrightarrow{{e}_{1}}}^{2}$+λ2${\overrightarrow{{e}_{2}}}^{2}$-2λ|$\overrightarrow{{e}_{1}}$||$\overrightarrow{{e}_{2}}$|cosθ,
即1+$\frac{1}{4}$+cosθ≤1+λ2-2λcosθ,即λ2-2λcosθ-($\frac{1}{4}$+cosθ)≥0恒成立,
∴△=4cos2θ+4($\frac{1}{4}$+cosθ)≤0,整理可得(cosθ+$\frac{1}{2}$)2≤0,
再由(cosθ+$\frac{1}{2}$)2≥0可得(cosθ+$\frac{1}{2}$)2=0,故cosθ=-$\frac{1}{2}$,
∵θ∈[0,π],∴θ=$\frac{2π}{3}$
故选:C
点评 本题考查向量的数量积和向量的夹角,涉及二次函数的性质,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{3}$ | B. | $\frac{9\sqrt{11}}{4}$ | C. | $\frac{16\sqrt{2}}{3}$ | D. | 18$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | lga>lgb |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
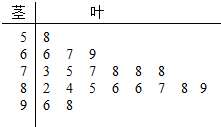 某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.
某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com