
双曲线的中心在坐标原点O,焦点在x轴上,过双曲线右焦点且斜率为![]() 的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.
的直线交双曲线于P、Q两点.若OP⊥OQ,|PQ|=4,求双曲线的方程.
|
解:设所求的双曲线方程为 y= 由 得 (5b2-3a2)x2|6a2cx-3a2c2-5a2b2=0. 设P(x1,y1),Q(x2,y2), 则x1+x2=- x1·x2= y1·y2= = = ∵OP⊥OQ,故kOP·kOQ=-1, ∴ 整理,得3a4+8a2b2-3b4=0, 亦即 (3a2-b2)(a2+3b2)=0. ∵a2+3b2≠0,∴b2=3a2. ① 由①,可推出c=2a, 设PQ的中点M的坐标为(x0,y0), 由 得 b2( ∴ ∵y1+y2=2y0,x1+x2=2x0, kPQ= ∴ 又M点在PQ上,故y0= 由②、③得x0=- ∵△OPQ是直角三角形,∴|OM|= ∴ ∴所求双曲线的方程为x2- 分析:如何根据题设条件OP⊥OQ,|PQ|=4,建立含a、b的方程组是解本题的关键.根据OP⊥OQ可得kOP·kOQ=-1,导出a、b的一个关系式.对已知|PQ|=4,可用弦长公式,也可利用Rt△OPQ斜边上的中线等于斜边的一半建立等量关系. 点评:解析几何中直线垂直关系通常转换为直线斜率的关系,直线被圆锥曲线截得线段长通常可用弦长公式建立等量关系.本题充分利用图形几何性质起到了简化运算的作用. |


科目:高中数学 来源: 题型:
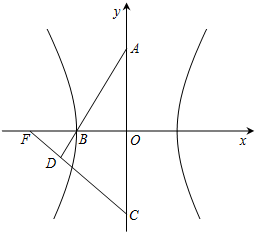 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
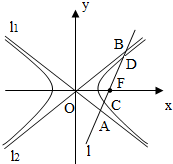 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率e=
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率e=
| ||
| 2 |
| OA |
| AB |
| OB |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com