
如图,设抛物线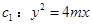 (
(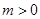 )的准线与
)的准线与 轴交于
轴交于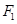 ,焦点为
,焦点为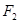 ;以
;以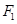 、
、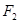 为焦点,离心率
为焦点,离心率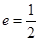 的椭圆
的椭圆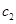 与抛物线
与抛物线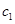 在
在 轴上方的一个交点为
轴上方的一个交点为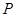 .
.
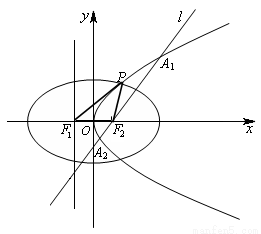
(1)当 时,求椭圆的方程;
时,求椭圆的方程;
(2)在(1)的条件下,直线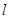 经过椭圆
经过椭圆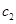 的右焦点
的右焦点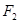 ,与抛物线
,与抛物线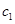 交于
交于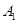 、
、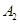 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点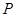 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由;
(3)是否存在实数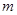 ,使得
,使得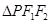 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数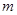 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)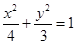 (2)即点
(2)即点 可在圆内,圆上或圆外
可在圆内,圆上或圆外
(3)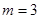 时,能使
时,能使 的边长是连续的自然数
的边长是连续的自然数
【解析】
解:∵ 的右焦点
的右焦点 ∴椭圆的半焦距
∴椭圆的半焦距 ,又
,又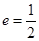 ,
,
∴椭圆的长半轴的长 ,短半轴的长
,短半轴的长 . 椭圆方程为
. 椭圆方程为 .
.
(1)当 时,故椭圆方程为
时,故椭圆方程为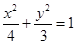 , 3分
, 3分
(2)依题意设直线 的方程为:
的方程为: ,
,
联立 得点
得点 的坐标为
的坐标为 .
.
将 代入
代入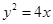 得
得 .
.
设 、
、 ,由韦达定理得
,由韦达定理得 ,
, .
.
又 ,
, .
.


∵ ,于是
,于是 的值可能小于零,等于零,大于零。
的值可能小于零,等于零,大于零。
即点 可在圆内,圆上或圆外. ………………………………9分
可在圆内,圆上或圆外. ………………………………9分
(3)假设存在满足条件的实数 , 由
, 由 解得:
解得: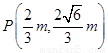 .
.
∴ ,
, ,又
,又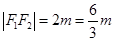 .
.
即 的边长分别是
的边长分别是 、
、 、
、 .
∴
.
∴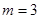 时,能使
时,能使 的边长是连续的自然数。 14分
的边长是连续的自然数。 14分
考点:椭圆的方程,直线与椭圆的位置关系
点评:解决该试题的关键是熟练的运用椭圆的简单几何性质来求解参数a,b,c的值,得到方程,并利用联立方程组的思想求解弦长,抛物线的定义是解决的关键点。属于基础题。


科目:高中数学 来源: 题型:
 如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为
如图,设抛物线C:y=x2的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
| ||
| 10 |
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源:汕头市2009-2010学年度第二学期高三级数学综合测练题(理二) 题型:解答题
(本题满分14分)如图,设抛物线 (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为 ,以
,以 、
、 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆 与抛物线
与抛物线 在
在 轴上方的一个交点为
轴上方的一个交点为 .
.
(1)当 时,求椭圆的方程;
时,求椭圆的方程;
(2)在(1)的条件下,直线 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与抛物线
,与抛物线 交于
交于 、
、 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由;
 (3)是否存在实数
(3)是否存在实数 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,设抛物线C1:![]() 的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率
的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率![]() 的椭圆C2与抛物线C1在x轴上方的交点为P。
的椭圆C2与抛物线C1在x轴上方的交点为P。
当m = 1时,求椭圆C2的方程;
 当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在
当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在![]() 上的一系列圆,它们的圆心纵坐标分别为a1,a2……an,已知a1 = 6,a1 > a2 >……> an > 0,又⊙Ck(k = 1,2,…,n)都与y轴相切,且顺次逐个相邻外切,求数列{an}的通项公式.
上的一系列圆,它们的圆心纵坐标分别为a1,a2……an,已知a1 = 6,a1 > a2 >……> an > 0,又⊙Ck(k = 1,2,…,n)都与y轴相切,且顺次逐个相邻外切,求数列{an}的通项公式.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com