
分析 (1)利用二倍角余弦公式的变形、两角和的正弦公式化简解析式,由三角函数的周期公式函数f(x)的最小正周期,由正弦函数的单调区间求出f(x)的递减区间;
(2)由x的范围求出$2x+\frac{π}{3}$的范围,由正弦函数的最值求出f(x)的最大值,由恒成立列出不等式,求出实数m的取值范围;
(3)由(1)化简f(α)=$\frac{11}{5}$,由α的范围求出2α+$\frac{π}{3}$的范围,由平方关系求出$cos(2α+\frac{π}{3})$,由两角差的余弦公式求出cos2α的值.
解答 解:(1)由题意得,f(x)=2sin2($\frac{π}{4}$-x)-$\sqrt{3}$cos2x
=1-cos($\frac{π}{2}$-2x)-$\sqrt{3}$cos2x=-sin2x-$\sqrt{3}$cos2x+1
=$-2sin(2x+\frac{π}{3})+1$,
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$,
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{3}≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{5π}{12}+kπ≤x≤\frac{π}{12}+kπ(k∈Z)$,
∴f(x)的单调递减区间是$[-\frac{5π}{12}+kπ,\frac{π}{12}+kπ](k∈Z)$;
(2)由x∈$[0,\frac{π}{6}]$得,$2x+\frac{π}{3}∈[\frac{π}{3},\frac{2π}{3}]$,
∴当$2x+\frac{π}{3}=\frac{π}{3}$时,函数f(x)取到最大值是$-\sqrt{3}+1$,
∵f(x)<m+2对x∈[0,$\frac{π}{6}$]恒成立,∴$-\sqrt{3}+1$<m+2,
解得m>$-\sqrt{3}-1$,
∴实数m的取值范围($-\sqrt{3}-1$,+∞);
(3)由(1)得,f(α)=$-2sin(2α+\frac{π}{3})+1$=$\frac{11}{5}$,
化简得,$sin(2α+\frac{π}{3})=-\frac{3}{5}$,
由$\frac{π}{3}$<α<$\frac{π}{2}$得,π<2α+$\frac{π}{3}$<$\frac{4π}{3}$,
∴$cos(2α+\frac{π}{3})$=$-\sqrt{1-si{n}^{2}(2α+\frac{π}{3})}$=$-\frac{4}{5}$,
∴cos2α=cos[(2α$+\frac{π}{3}$)-$\frac{π}{3}$]=cos$(2α+\frac{π}{3})$ cos$\frac{π}{3}$+sin $(2α+\frac{π}{3})$ sin$\frac{π}{3}$
=$-\frac{4}{5}×\frac{1}{2}+(-\frac{3}{5})×\frac{\sqrt{3}}{2}$=$\frac{-4-3\sqrt{3}}{10}$.
点评 本题考查正弦函数的图象与性质,三角恒等变换中的公式在化简、求值中的应用,以及恒成立问题的转化,注意角的范围和三角函数值的符号,考查转化思想,化简变形、计算能力.


科目:高中数学 来源: 题型:解答题
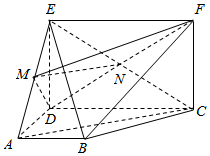 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.
如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com