��������1����������-��x+1��
2+a��x+1����2��-
2+ax����һ��[3��+�ޣ��������ת��Ϊa
��=
=��x-1��
-�����û�������ʽ��⼴�ɣ�
��2����������f�ó�f��x����[0��+�ޣ��ϵ���������m��0��m
n•2
n-n��m
n-1•2
n-��n-1������m��2��
��3����x��[4n��4n+4]��n��Zʱ��f��x��=mf��x-4��=��=m
nf��x-4n��=m
n[��x-4n��
2-4��x-4n��]�������-1��m��0��0��m��1��
���
�⣺��1���������֪��f��x+1����2f��x����
��-��x+1��
2+a��x+1����2��-
2+ax����һ��[3��+�ޣ��������
��x-1��a��x
2-2x-1��
��x��[3��+�ޣ�
��a
��=
=��x-1��
-��
��x-1=t����t��[2��+�ޣ���
g��x��=t
-��[2��+�ޣ��ϵ���������
��g��t��
min=g��2��=1��
��a��1��
��2����x��[0��1��ʱ��f��x��=2
x��
�൱x��[1��2��ʱ��f��x��=mf��x-1��=m•2
x-1��
��x��[n��n+1]ʱ��f��x��=mf��x-1��=m
2f��x-2��=��=m
nf��x-n��=m
n•2
x-n��
��x��[n��n+1��ʱ��f��x��=m
n•2
x-n��n��N
*��
��f��x����[0��+�ޣ��ϵ���������
��m��0��m
n•2
n-n��m
n-1•2
n-��n-1������m��2��
��3�����⣨�ߵ�x��[0��4]ʱ��y��[-4��0]������f��x+4��=mf��x����
�൱x��[4n��4n+4]��n��Zʱ��
f��x��=mf��x-4��=��=m
nf��x-4n��=m
n[��x-4n��
2-4��x-4n��]��
��0��m��1ʱ��f��x����[-4��0]��
��-1��m��0ʱ��f��x����[-4��-4m]��
��m=-1ʱ��f��x����[-4��4]��
��m��1ʱ��f��x���ʣ�-�ޣ�0����
��m��-1ʱ��f��x���ʣ�-�ޣ�+�ޣ���
���Ͽ�֪��-1��m��0��0��m��1��
���⣨������֪����f��x+T��=T•f��x����һ��ʵ��x�������
��cosk��x+T��=Tcoskx��һ��ʵ���������
��k=0ʱ��T=1��
��k��0ʱ����x��R����kx��R��kx+kT��R������coskx��[-1��1]��
�֡�cos��kx+kT����[-1��1]��
��Ҫʹcosk��x+T��=Tcoskx�������ֻ��T=��1��
��T=1ʱ��cos��kx-k��=coskx �õ� k=2n�У�n����n��0��
��T=-1ʱ��cos��kx-k��=-coskx �õ�-k=2n��+�У�
��k=��2n+1����n��Z��
���Ͽ�֪����T=1ʱ��k=2n�У�n��Z��
��T=-1ʱ��K=��2n+1���У�n��Z��




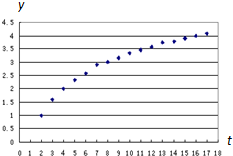 ij�о�С����һ��ʵ���л��һ�����y��t֮������ݣ�����������õ���ͼ��ʾ��ɢ��ͼ�����к����У����ܽ��ƿ̻�y��t֮���ϵ���ǣ�������
ij�о�С����һ��ʵ���л��һ�����y��t֮������ݣ�����������õ���ͼ��ʾ��ɢ��ͼ�����к����У����ܽ��ƿ̻�y��t֮���ϵ���ǣ�������