
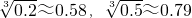 ,0.582=0.3364,0.792=0.6241)
,0.582=0.3364,0.792=0.6241)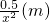 ,
,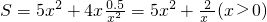
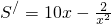 ,
,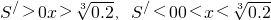 ,
,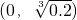 上递减,在
上递减,在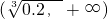 上递增,
上递增,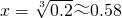 时,S有最小值,此时
时,S有最小值,此时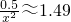
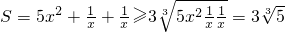 (当且仅当
(当且仅当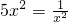 即
即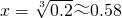 时,取等号)
时,取等号)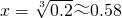 时,S有最小值
时,S有最小值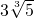 ,此时
,此时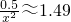
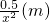 ,得出
,得出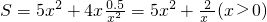
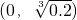 上递减,在
上递减,在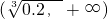 上递增,得到函数的最小值即可;
上递增,得到函数的最小值即可;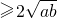 当且仅当a=b时取等号的方法求出此时的x值并求出高即可.
当且仅当a=b时取等号的方法求出此时的x值并求出高即可.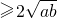 当且仅当a=b时取等号的方法求函数最值的能力.
当且仅当a=b时取等号的方法求函数最值的能力. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 | 0.2 |
| 3 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设计一种正四棱柱形冰箱,它有一个冷冻室和一个冷藏室,冷藏室用两层隔板分为三个抽屉,问:如何设计它的外形尺寸,能使得冰箱体积![]() 为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小
为定值时,它的表面和三层隔板(包括冷冻室的底层)面积之和S值最小![]() (参考数据:
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源:2010年山东省日照实验高中高考数学综合练习试卷8(理科)(解析版) 题型:解答题
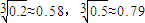 ,0.582=0.3364,0.792=0.6241)
,0.582=0.3364,0.792=0.6241)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com