
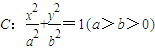 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为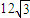 .w
.w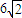 ,试判断△MAB的形状.
,试判断△MAB的形状.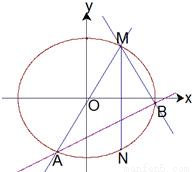
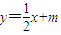 (m∈R),代入b2x2+a2y2=a2b2得:
(m∈R),代入b2x2+a2y2=a2b2得: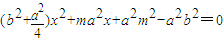 设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R),则
设A(x1,y1),B(x2,y2)(x1,2,y1,2∈R),则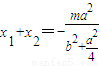 ,
,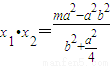 ,再由
,再由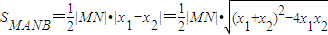 =
=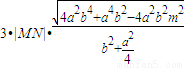 能求出椭圆C的方程.
能求出椭圆C的方程.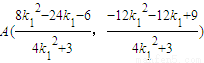 ,同理:
,同理: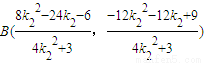 ,所以
,所以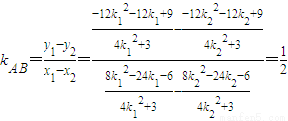 ,由此能够证明△MAB直角三角形.
,由此能够证明△MAB直角三角形.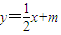 (m∈R),
(m∈R), ,
,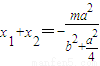 ,
,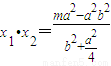 ,------(3分)
,------(3分)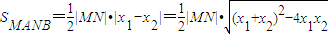
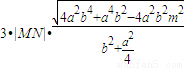 ,
,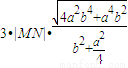 =
=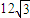 (1)
(1) .(4)------(7分)
.(4)------(7分)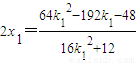 ,
,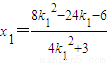
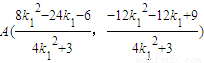
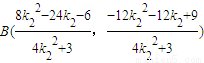
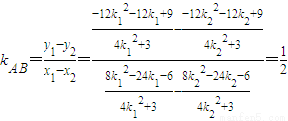 ------(12分)
------(12分)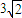 ,
, ,
, .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
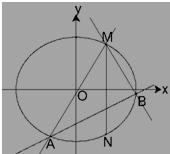 已知两点M(2,3),N(2,-3)在椭圆C:
已知两点M(2,3),N(2,-3)在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
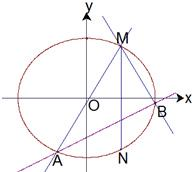 (2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆C:
(2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳市东北育才学校高三(下)4月月考数学试卷(理科)(解析版) 题型:解答题
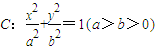 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为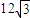 .求椭圆C的方程.
.求椭圆C的方程.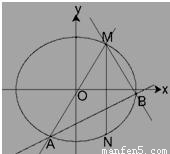
查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷2(理科)(解析版) 题型:解答题
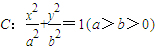 上,斜率为
上,斜率为 的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为
的直线l与椭圆C交于点A,B(A,B在直线MN两侧),且四边形MANB面积的最大值为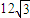 .w
.w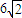 ,试判断△MAB的形状.
,试判断△MAB的形状.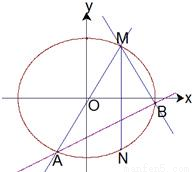
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com