【答案】
分析:设出三向量的模分别为a,b及c,根据周长为6列出关于a+b+c=6,再由a,b及c成等边数列,根据等比数列的性质得到b
2=ac,然后由余弦定理表示出cosB,把b
2=ac代入,并利用基本不等式求出cosB的最小值,根据余弦函数的图象得到B的范围,同时由b=
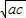
及基本不等式列出关于b的不等式,求出不等式的解集得到b的范围,根据三角形的两边之差小于第三边列出不等式,由三角形的周长及b
2=ac,得到关于b的一元二次不等式,求出不等式的解集可得b的范围,由a,b及sinB,根据三角形的面积公式表示出三角形ABC的面积,把ac化为b
2后,根据b的最大值及B度数的最大值,得到S的最大值即可.
解答:解:依次为a,b,c,则a+b+c=6,b
2=ac,
由余弦定理得:cosB=
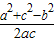
=
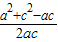
≥
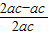
=

,
∴0<B≤
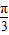
,
又b=
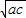
≤
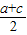
=
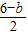
,从而0<b≤2,
∵△ABC三边依次为a,b,c,则a-c<b,即有(a-c)
2<b
2,
∵a+b+c=6,b
2=ac,b
2>(a+c)
2-4ac,
∴b
2+3b-9>0,b>
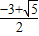
,
∴
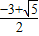
<b≤2,
∴S=

acsinB=

b
2•sinB≤

•2
2•sin
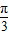
=
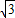
,
则S的最大值为
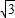
.
故选C
点评:此题属于解三角形的题型,涉及的知识有等比数列的性质,余弦定理,基本不等式,一元二次不等式的解法,三角形的面积公式,平面向量的数量积运算,以及二次函数最值的求法,其中根据余弦定理,等比数列的性质及不等式的解法得出B及b的范围是解本题的关键.

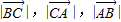 成等比数列,求△ABC的面积S的最大值( )
成等比数列,求△ABC的面积S的最大值( )
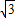
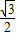
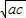 及基本不等式列出关于b的不等式,求出不等式的解集得到b的范围,根据三角形的两边之差小于第三边列出不等式,由三角形的周长及b2=ac,得到关于b的一元二次不等式,求出不等式的解集可得b的范围,由a,b及sinB,根据三角形的面积公式表示出三角形ABC的面积,把ac化为b2后,根据b的最大值及B度数的最大值,得到S的最大值即可.
及基本不等式列出关于b的不等式,求出不等式的解集得到b的范围,根据三角形的两边之差小于第三边列出不等式,由三角形的周长及b2=ac,得到关于b的一元二次不等式,求出不等式的解集可得b的范围,由a,b及sinB,根据三角形的面积公式表示出三角形ABC的面积,把ac化为b2后,根据b的最大值及B度数的最大值,得到S的最大值即可.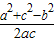 =
=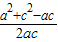 ≥
≥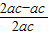 =
= ,
,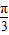 ,
,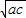 ≤
≤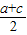 =
=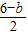 ,从而0<b≤2,
,从而0<b≤2,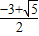 ,
,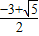 <b≤2,
<b≤2, acsinB=
acsinB= b2•sinB≤
b2•sinB≤ •22•sin
•22•sin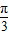 =
=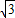 ,
,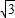 .
.

 阅读快车系列答案
阅读快车系列答案