
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
某初级中学有学生270人,其中一年级108人,二、三年级各81人,利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生一、二、三年级依次统一编号为 1,2, …,270; 使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段。如果抽得号码有下列四种情况:
①7,9,100,107,111, 121, 180,197,200,265;
②6,33,60,87,114, 141,168,195,222,249;
③30,57,84,111,138, 165, 192, 219,246,270.
④12,39,66,93,120, 147, 174,201,228,255;
关于上述样本的下列结论中,正确的是 ( )
A. ①④都不能为系统抽样 B. ①③都不能为分层抽样
C. ②④都可能为分层抽样 D. ②③都可能为系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
| 合计 | 20 | 1 |
(Ⅰ) 根据上面的频率分布表,估计该居民区PM2.5的24小时平均浓度超过50微克/立方米的概率;
(Ⅱ)计算样本众数、中位数和平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD .
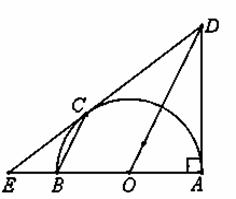
(Ⅰ)求证:DE是圆O的切线;
(Ⅱ)如果AD =AB = 2,求EB .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com