
已知关于 的一次函数
的一次函数
(1)设集合 和
和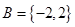 ,分别从集合
,分别从集合 和
和 中随机取一个数作为
中随机取一个数作为 ,
, ,求函数
,求函数 是增函数的概率;
是增函数的概率;
(2)若实数 ,
, 满足条件
满足条件 ,求函数
,求函数 的图象不经过第四象限的概率.
的图象不经过第四象限的概率.
(1)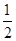 ;(2)
;(2)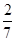
解析试题分析:(1)依题意,基本事件总数为8个,记“函数 是增函数”为事件A,则
是增函数”为事件A,则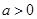 ,事件A包含的基本事件分别为:
,事件A包含的基本事件分别为: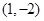 ,
,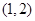 ,
, ,
,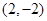 ,共4个,由古典概型的概率计算公式得,所求概率为
,共4个,由古典概型的概率计算公式得,所求概率为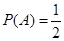 ;(2)本题还有两个变量,基本事件用有序实数对
;(2)本题还有两个变量,基本事件用有序实数对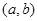 表示,画出不等式表示的平面区域,即基本事件空间,因为函数
表示,画出不等式表示的平面区域,即基本事件空间,因为函数 的图象不经过第四象限,则满足
的图象不经过第四象限,则满足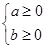 ,由几何概型的概率计算公式,可计算其面积的比即为概率.
,由几何概型的概率计算公式,可计算其面积的比即为概率.
试题解析:(1)抽取全部结果所构成的基本事件空间为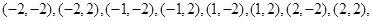 共8个4分
共8个4分
设函数是增函数为事件 ,
,
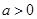 ,有4个
,有4个
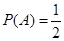 7分
7分
(2)实数 ,
, 满足条件
满足条件 ,要函数
,要函数 的图象不经过第四象限
的图象不经过第四象限
则需使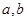 满足
满足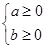 ,即
,即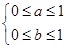 , 10分
, 10分
设“函数 的图象不经过第四象限”为事件B,则
的图象不经过第四象限”为事件B,则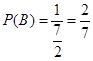 .
.
考点:1、一次函数的图象;2、古典概型;3、几何概型.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间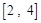 的有8人.
的有8人.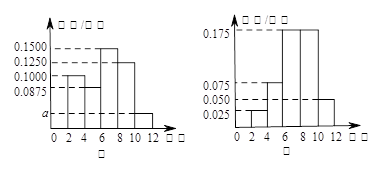
(1)求直方图中 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间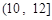 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为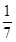 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(1)求袋中原有白球的个数;
(2)求随机变量ξ的概率分布;
(3)求甲取到白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 大于40岁 | 16 | | |
| 小于等于40岁 | | 12 | |
| 合计 | | | 40 |
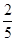
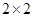 列联表补充完整;
列联表补充完整;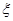 ,求
,求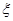 的分布列和数学期望;
的分布列和数学期望;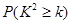 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
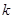 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
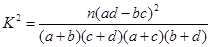 ,其中
,其中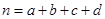 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
| 答对题目数 |  | 8 | 9 |  |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“蛟龙号”从海底中带回的某种生物,甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究,每次试验一个生物,甲组能使生物成活的概率为 ,乙组能使生物成活的概率为
,乙组能使生物成活的概率为 ,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
(1)甲小组做了三次试验,求至少两次试验成功的概率;
(2)如果乙小组成功了4次才停止试验,求乙小组第四次成功前共有三次失败,且恰有两次连续失败的概率;
(3)若甲乙两小组各进行2次试验,设试验成功的总次数为 ,求
,求 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
箱子里有3双不同的手套,随机拿出2只,记事件A表示“拿出的手套配不成对”;事件B表示“拿出的都是同一只手上的手套”.
(1)请列出所有的基本事件;
(2)分别求事件A、事件B的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“抛阶砖”是国外游乐场的典型游戏之一.参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏但很少有人得到奖品,请用所学的概率知识解释这是为什么.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com