
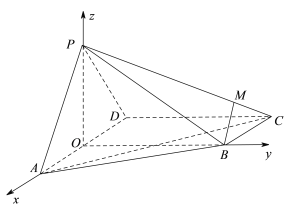
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值?若不存在,说明理由.
的值?若不存在,说明理由.
【答案】(1)见解析;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】
(1)利用面面垂直的性质得到线面垂直,再由线面垂直的性质得出![]() ;
;
(2)建立空间直角坐标系,利用向量法求解即可;
(3)由![]() ,C,M三点共线,利用向量共线得出
,C,M三点共线,利用向量共线得出![]() ,利用线面垂直的判定定理证明平面
,利用线面垂直的判定定理证明平面![]() ,由于
,由于![]() ,
,![]() 不平行,则不存在棱
不平行,则不存在棱![]() 上的点
上的点![]() ,使得
,使得![]() 平面
平面![]() .
.
(1)在四棱锥![]() 中
中
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
又因为![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以![]()
(2)取![]() 中点
中点![]() ,连接
,连接![]()
因为![]()
所以![]()
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
所以![]()
因为![]()
所以![]()
所以四边形![]() 是平行四边形
是平行四边形
所以![]()
如图建立空间直角坐标系![]() ,则
,则
![]()
![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
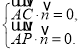 即
即![]()
令![]() ,则
,则![]() .
.
所以![]() .
.
因为平面![]() 的法向量
的法向量![]() ,
,
所以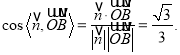
由图可知,二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)设![]() 是棱
是棱![]() 上一点,则存在
上一点,则存在![]() 使得
使得![]() .
.
设![]() ,则
,则![]()
所以![]()
所以![]()
所以![]() .
.
所以![]() .
.
因为![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
若![]() 平面
平面![]() ,则
,则![]() .
.
所以![]()
因为方程组无解,
所以在棱![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,如果存在实数
,如果存在实数![]() (
(![]() ,且
,且![]() 不同时成立),使得
不同时成立),使得![]() 对
对![]() 恒成立,则称函数
恒成立,则称函数![]() 为“
为“![]() 映像函数”.
映像函数”.
(1)判断函数![]() 是否是“
是否是“![]() 映像函数”,如果是,请求出相应的
映像函数”,如果是,请求出相应的![]() 的值,若不是,请说明理由;
的值,若不是,请说明理由;
(2)已知函数![]() 是定义在
是定义在![]() 上的“
上的“![]() 映像函数”,且当
映像函数”,且当![]() 时,
时,![]() .求函数
.求函数![]() (
(![]() )的反函数;
)的反函数;
(3)在(2)的条件下,试构造一个数列![]() ,使得当
,使得当![]() 时,
时,![]() ,并求
,并求![]() 时,函数
时,函数![]() 的解析式,及
的解析式,及![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半圆![]() 的直径的两端点为
的直径的两端点为![]() ,点
,点![]() 在半圆
在半圆![]() 及直径
及直径![]() 上运动,若将点
上运动,若将点![]() 的纵坐标伸长到原来的2倍(横坐标不变)得到点
的纵坐标伸长到原来的2倍(横坐标不变)得到点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线![]() 的“直径”.
的“直径”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在该空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
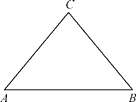
(1) 若小路一端E为AC的中点,求此时小路的长度;
(2) 求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)对于大于![]() 的正整数
的正整数![]() 、
、![]() (其中
(其中![]() ),若
),若![]() 、
、![]() 、
、![]() 三个数经适当排序后能构成等差数列,求符合条件的数组
三个数经适当排序后能构成等差数列,求符合条件的数组![]() ;
;
(3)若数列![]() 满足
满足![]() ,是否存在实数
,是否存在实数![]() ,使得数列
,使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,给定
,给定![]() 个整点
个整点![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,从上面的
时,从上面的![]() 个整点中任取两个不同的整点
个整点中任取两个不同的整点![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)从上面![]() 个整点中任取
个整点中任取![]() 个不同的整点,
个不同的整点,![]() .
.
(i)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() ;
;
(ii)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,沿河有A、B两城镇,它们相距![]() 千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为
千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为![]() (万元),
(万元),![]() 表示污水流量;铺设管道的费用(包括管道费)
表示污水流量;铺设管道的费用(包括管道费)![]() (万元),
(万元),![]() 表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为
表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为![]() 、
、![]() ,
,![]() 、
、![]() 两城镇连接污水处理厂的管道总长为
两城镇连接污水处理厂的管道总长为![]() 千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到
千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到![]() ):
):

(1)若在城镇A和城镇B单独建厂,共需多少总费用?
(2)考虑联合建厂可能节约总投资,设城镇A到拟建厂的距离为![]() 千米,求联合建厂的总费用
千米,求联合建厂的总费用![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com