在△ABC的角A,B,C所对的边分别是a,b,c.虚数x=2+ai是实系数方程x2-cx+8=0的根.
(1)求边长a,c.
(2)若边长a,b,c成等比数列,求△ABC的面积.
【答案】
分析:(1)易得x
1=2+a与x
2=2-a是实系数方程x
2-cx+8=0的两个根,由韦达定理可得答案;
(2)由等比数列易得b值,进而由余弦定理可得cosB,sinB,代入面积公式即可.
解答:解:(1)由题意可得虚数x
1=2+a与x
2=2-a是实系数方程x
2-cx+8=0的两个根.----------(2分)
由根与系数的关系可得
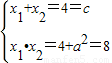
-------------------------------------------------------------------(4分)
解得
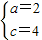
--------------------------------------------------------------------------------(6分)
(2)∵边长a,b,c成等比数列,∴b
2=ac,解得b=
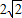
----------------(7分)
根据余弦定理cosB=
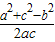
=
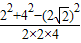
=

---------------------------------------(9分)
由同角三角函数的基本关系可得sinB=
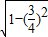
=
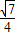
---------------------------------------------------------------------------(10分)
所以S
△ABC=
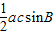
=
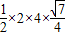
=
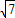
---------------------------------------------------------(12分)
点评:本题考查实系数的一元二次方程的根,涉及复数的运算和等比数列的性质,以及三角函数的运算,属基础题.

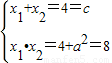 -------------------------------------------------------------------(4分)
-------------------------------------------------------------------(4分)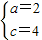 --------------------------------------------------------------------------------(6分)
--------------------------------------------------------------------------------(6分)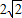 ----------------(7分)
----------------(7分)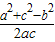 =
=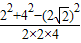 =
= ---------------------------------------(9分)
---------------------------------------(9分)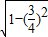 =
=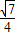 ---------------------------------------------------------------------------(10分)
---------------------------------------------------------------------------(10分)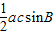 =
=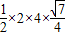 =
=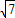 ---------------------------------------------------------(12分)
---------------------------------------------------------(12分)

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案