
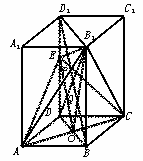
图10-23
(Ⅰ)求截面EAC的面积;
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ)求三棱锥B1-EAC的体积.
(Ⅰ)解:如图10-55,连结DB交AC于O,连结EO.
∵底面ABCD是正方形,

图10-55
∴DO⊥AC 又∵ED⊥底面AC, ∴EO⊥AC.
∴∠EOD是面EAC与底面AC所成二面角的平面角,
∴∠EOD=45°
DO=![]() a,AC=
a,AC=![]() a,EO=
a,EO=![]() asec45°=a,
asec45°=a,
故S△EAC=![]() a2.
a2.
(Ⅱ)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC.
又A1A⊥A1B1,
∴A1A是异面直线A1B1与AC间的公垂线.
∵D1B∥面EAC,且面D1BD与面EAC交线为EO,
∴D1B∥EO又O是DB的中点.
∴E是D1D的中点,D1B=2EO=2a.
∴D1D=![]() =
=![]() a异面直线A1B1与AC间的距离为
a异面直线A1B1与AC间的距离为![]() a.
a.
(Ⅲ)方法一:如图10-56,连结D1B1.

图10-56
∵D1D=DB=![]() a,
a,
∴BDD1B1是正方形连结B1D交D1B于P,交EO于Q
∵B1D⊥D1B,EO∥D1B,∴B1D⊥EO.
又AC⊥EO,AC⊥ED.
∴AC⊥面BDD1B1,∴B1D⊥AC,
∴B1D⊥面EAC.∴B1Q是三棱锥B1-EAC的高.
由DQ=PQ,得B1Q=![]() B1D=
B1D=![]() a
a
∴VB1-EAC=![]() ·
·![]() a2·
a2·![]() a=
a=![]() a3.
a3.
所以三棱锥B1-EAC的体积是![]() a3.
a3.
方法二:连结B1O,则VB1-EAC=2VA-EOB1
∵AO⊥面BDD1B1,
∴AO是三棱锥A-EOB1的高,AO=![]() a
a
在正方形BDD1B1中,E、O分别是D1D、DB的中点,则
S△EOB1=![]() a2
a2
∴VB1-EAC=2·![]() ·
·![]() a2·
a2·![]() a=
a=![]() a3.
a3.
所以三棱锥B1-EAC的体积是![]() a3.
a3.


科目:高中数学 来源: 题型:

图10-23
(Ⅰ)求截面EAC的面积;
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ)求三棱锥B1-EAC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线![]() 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为![]() ,求|PA|+|PB|.
,求|PA|+|PB|.
23(本小题满分10分)
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,![]() ,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
24.(本小题满分10分)
将一枚硬币连续抛掷![]() 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为![]() ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为![]() .
.
(Ⅰ)若该硬币均匀,试求![]() 与
与![]() ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线![]() 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为![]() ,求|PA|+|PB|.
,求|PA|+|PB|.
23(本小题满分10分)
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,![]() ,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
24.(本小题满分10分)
将一枚硬币连续抛掷![]() 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为![]() ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为![]() .
.
(Ⅰ)若该硬币均匀,试求![]() 与
与![]() ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com