
| ���� | ������ | �ܼ� | |
| �װ� | |||
| �Ұ� | 30 | ||
| �ܼ� | 60 |
| 1 |
| 2 |
| 1 |
| 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 110��(40��30-20��20)2 |
| 60��50��60��50 |
| ���� | ������ | �ܼ� | |
| �װ� | 40 | 20 | 60 |
| �Ұ� | 20 | 30 | 50 |
| �ܼ� | 60 | 50 | 110 |
| 110��(40��30-20��20)2 |
| 60��50��60��50 |
| 1 |
| 2 |
| 1 |
| 3 |
. |
| M |
. |
| N |
. |
| R |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
. |
| N |
. |
| R |
. |
| M |
. |
| R |
. |
| M |
. |
| N |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
. |
| R |
. |
| M |
. |
| N |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 18 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 18 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 9 |
| 4 |
| 9 |
| 5 |
| 18 |
| 1 |
| 18 |
| 7 |
| 6 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
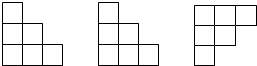 ��֪���ɸ�������Сľ��ѷ���һ���γɵ�����������ͼ��ͼ��ʾ��������Сľ�������ж��ٸ���������
��֪���ɸ�������Сľ��ѷ���һ���γɵ�����������ͼ��ͼ��ʾ��������Сľ�������ж��ٸ���������| A��7�� | B��8�� | C��9�� | D��10�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| A��3 | B��2 | C��1 | D��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
| 3 |
| x2 |
| x1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 2 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| y |
| 1 |
| x |
| x |
| y |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com