
(2012年高考(四川理))已知![]() 为正实数,
为正实数,![]() 为自然数,抛物线
为自然数,抛物线![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,设
,设![]() 为该抛物线在点
为该抛物线在点![]() 处的切线在
处的切线在![]() 轴上的截距.
轴上的截距.
(Ⅰ)用![]() 和
和![]() 表示
表示![]() ;
;
(Ⅱ)求对所有![]() 都有
都有![]() 成立的
成立的![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【解析】(1)由已知得,交点A的坐标为 ,对
,对![]() 则抛物线在点A处的切线方程为
则抛物线在点A处的切线方程为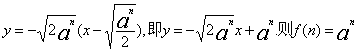
(2)由(1)知f(n)=![]() ,则
,则![]()
即知,![]() 对于所有的n成立,特别地,取n=2时,得到a≥
对于所有的n成立,特别地,取n=2时,得到a≥![]()
当![]() ,
,
![]()
![]()
![]()
![]()
>2n3+1
当n=0,1,2时,显然![]()
故当a=![]() 时,
时,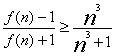 对所有自然数都成立
对所有自然数都成立
所以满足条件的a的最小值是![]() .
.
(3)由(1)知![]() ,则
,则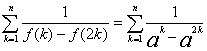 ,
,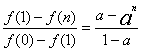
下面证明:![]()
首先证明:当0<x<1时,![]()
设函数![]()
![]()
当![]()
故g(x)在区间(0,1)上的最小值g(x)min=g![]()
所以,当0<x<1时,g(x)≥0,即得![]()
由0<a<1知0<ak<1(![]() ),因此
),因此![]() ,从而
,从而
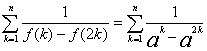
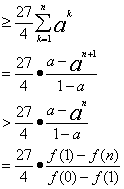
【点评】本小题属于高档题,难度较大,需要考生具备扎实的数学基础和解决数学问题的能力.主要考查了导数的应用、不等式、数列等基础知识;考查了思维能力、运算能力、分析问题与解决问题的能力和创新意识能力;且又深层次的考查了函数、转换与化归、特殊与一般等数学思维方法.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
(2012年高考(江西理))如图,已知正四棱锥S-ABCD所有棱长都为1,点E是侧棱SC上一动点,过点E垂直于SC的截面将正四棱锥分成上、下两部分.记SE=x(0<x<1),截面下面部分的体积为V(x),则函数y=V(x)的图像大致为


查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考山东卷理科10)已知椭圆C:![]() 的离心率为
的离心率为![]() ,双曲线x²-y²=1的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为
,双曲线x²-y²=1的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com