
 11、如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=70°,则∠CBE=
11、如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是CE与⊙O的交点.若∠BAC=70°,则∠CBE=科目:高中数学 来源: 题型:
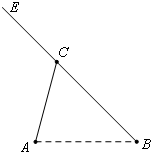 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.| 2 |
| 3 |
| 6 |
| 331 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选修4-1:几何证明选讲
选修4-1:几何证明选讲查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com