
(本题满分15分)过点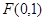 作直线
作直线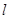 与抛物线
与抛物线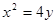 相交于两点
相交于两点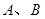 ,圆
,圆
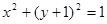
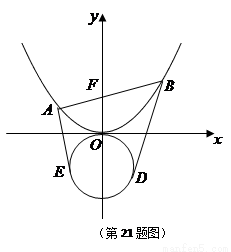
(Ⅰ)若抛物线在点 处的切线恰好与圆
处的切线恰好与圆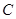 相切,求直线
相切,求直线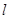 的方程;
的方程;
(Ⅱ)过点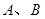 分别作圆
分别作圆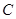 的切线
的切线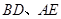 ,试求
,试求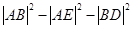 的取值范围.
的取值范围.
(I)直线 的方程为:
的方程为: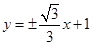 .(Ⅱ)
.(Ⅱ)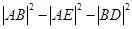 的取值范围是
的取值范围是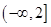 .
.
【解析】本试题主要是考查了直线与抛物线于圆与直线的位置关系的综合运用。以及导数的几何意义的运用,以及勾股定理的综合运用。
(1)利用导数的几何意义表示切线方程,以及直线与圆相切,则圆心到直线的距离为圆的半径可以得到结论。
(2)设出直线与抛物线联立方程组,结合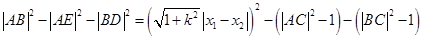
和韦达定理得到坐标关系,然后求解取值范围。
解:设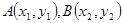
由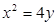 ,得
,得 过点
过点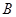 的切线方程为:
的切线方程为:
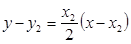 ,即
,即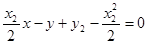 (3分)
(3分)
由已知: ,又
,又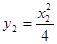 ,
(5分)
,
(5分)
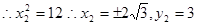 ,
,
即点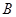 坐标为
坐标为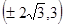 ,
(6分)
,
(6分)
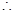 直线
直线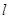 的方程为:
的方程为: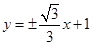 . (7分)
. (7分)
(Ⅱ)由已知,直线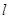 的斜率存在,则设直线
的斜率存在,则设直线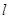 的方程为:
的方程为: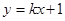 , (8分)
, (8分)
联立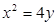 ,得
,得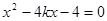
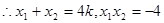
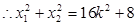 (9分)
(9分)
解法一: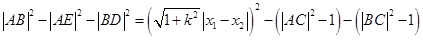 (12分)
(12分)


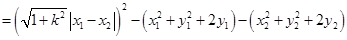
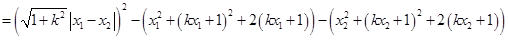 (13分)
(13分)
 =
=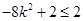 (15分)
(15分)
解法二: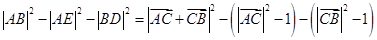 (12分)
(12分)
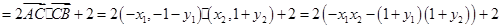
 (13分)
(13分)

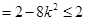 (15分)
(15分)
解法三: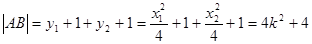 ,
,
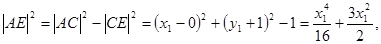
同理,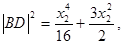 (13分)
(13分)
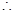
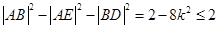
故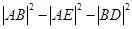 的取值范围是
的取值范围是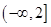 .
(15分)
.
(15分)


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
(本题满分15分)过![]() 轴上的动点
轴上的动点![]() ,引抛物线
,引抛物线![]() 两条切线
两条切线![]() ,
,![]() 为切点。
为切点。
(Ⅰ)求证:直线![]() 过定点
过定点![]() ,并求出定点
,并求出定点![]() 坐标;
坐标;
(Ⅱ)若![]() ,设弦
,设弦![]() 的中点为
的中点为![]() ,试求
,试求![]() 的最小值(
的最小值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市高三第一次适应性测试理科数学 题型:解答题
(本题满分15分)如图,在矩形 中,
中, 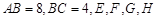 分别为四边
分别为四边
的中点,且都在坐标轴上,设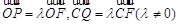 .
.
(Ⅰ)求直线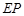 与
与 的交点
的交点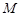 的轨迹
的轨迹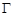 的方程;
的方程;
(Ⅱ)过圆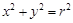
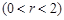 上一点
上一点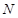 作圆的切线与轨迹
作圆的切线与轨迹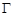 交于
交于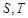 两点,若
两点,若 ,试求出
,试求出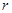 的值.
的值.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三第二学期第一次统考文科数学 题型:解答题
(本题满分15分) 设抛物线C1:x 2=4 y的焦点为F,曲线C2与C1关于原点对称.
(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足| AB |是 | FA | 与 | FB | 的等差中项?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三高考样卷数学文卷 题型:解答题
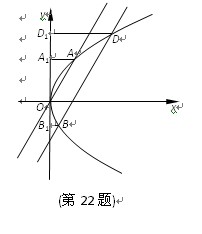
(本题满分15分) 已知直线l1:x=my与抛物线C:y2=4x交于O (坐标原点),A两点,直线l2:x=my+m 与抛物线C交于B,D两点.
(Ⅰ) 若 | BD | = 2 | OA |,求实数m的值;
(Ⅱ) 过A,B,D分别作y轴的垂线,垂足分别为A1,B1,D1.记S1,S2分别为三角形OAA1和四边形BB1D1D的面积,求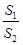 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com