
已知双曲线C1: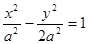 (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(1)求证:C1,C2总有两个不同的交点;
(2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。
(1)由双曲线方程得 ,所以F1(
,所以F1(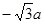 ,0),抛物线焦点到准线的距离
,0),抛物线焦点到准线的距离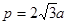 ,抛物线:
,抛物线: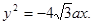 ①
①
把①代入C1方程得: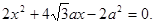 ②
②
Δ=64a2>0,所以方程②必有两个不同实根,设为x1,x2,由韦达定理得x1x2=-a2<0,所以②必有一个负根设为x1,把x1代入①得y2=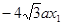 ,所以
,所以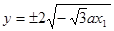 (因为x1≠0),所以C1,C2总有两个不同交点。
(因为x1≠0),所以C1,C2总有两个不同交点。
(2)设过F1(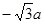 ,0)的直线AB为my=(x+
,0)的直线AB为my=(x+ a),由
a),由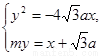 得y2+4
得y2+4 may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=
may-12a2=0,因为Δ=48m2a2+48a2>0,设y1,y2分别为A,B的纵坐标,则y1+y2=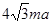 ,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=
,y1y2=-12a2.所以(y1-y2)2=48a2(m2+1).所以SΔAOB=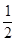 |y1-y2|•|OF1|=
|y1-y2|•|OF1|=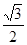 a•
a•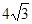 a•
a•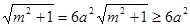 ,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=
,当且仅当m=0时,SΔAOB的面积取最小值;当m→+∞时,SΔAOB→+∞,无最大值。所以存在过F的直线x=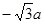 使ΔAOB面积有最小值6a2。
使ΔAOB面积有最小值6a2。
【解析】略


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:选择题
已知双曲线C1: -
- =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
(A)x2=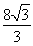 y (B)x2=
y (B)x2= y
y
(C)x2=8y (D)x2=16y
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练19练习卷(解析版) 题型:填空题
已知双曲线C1: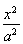 -
-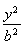 =1(a>0,b>0)与双曲线C2:
=1(a>0,b>0)与双曲线C2: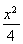 -
-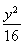 =1有相同的渐近线,且C1的右焦点为F(
=1有相同的渐近线,且C1的右焦点为F(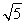 ,0),则a= ,b= .
,0),则a= ,b= .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北衡水中学高三上学期第五次调研考试文科数学试卷(解析版) 题型:选择题
已知双曲线C1: (a>0,b>0)的焦距是实轴长的2倍.若抛物线C2:
(a>0,b>0)的焦距是实轴长的2倍.若抛物线C2: (p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
A.x2= y B.x2=
y B.x2= y C.x2=8y D.x2=16y
y C.x2=8y D.x2=16y
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高考预测数学试卷:填空解答题(解析版) 题型:解答题
已知双曲线C1: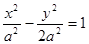 (a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(a>0),抛物线C2的顶点在原点O,C2的焦点是C1的左焦点F1。
(1)求证:C1,C2总有两个不同的交点;
(2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com