
|
| x2 |
| 4 |
|
| �� |
| 2 |
|
|
|
|
|
| x2 |
| 4 |
a2
| ||
| 4 |
| y | 20 |
|
|
| �� |
| 2 |
|
|
|
| ||
|
|4+2sin(
| ||
|
| �� |
| 3 |
| 2 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| x2 |
| 4 |
|
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| (a+b+c)2 |
| 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�긣��ʡ�����ڰ˴��¿�������ѧ�Ծ� ���ͣ������
�������У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14��
��1������С������7�֣�ѡ��4-2��������任
�任 �ǽ�ƽ����ÿ����
�ǽ�ƽ����ÿ���� �ĺ������
������ ���������
��������� ���䵽��
���䵽�� .
.
������任 �ľ���
�ľ���
����Բ �ڱ任
�ڱ任 �������±����ʲôͼ�Σ�
�������±����ʲôͼ�Σ�
��2������С������7�֣�ѡ��4-4������ϵ���������
��֪������ԭ���غϣ�������x����������غϣ������� �ļ����귽��Ϊ��
�ļ����귽��Ϊ�� ��ֱ��
��ֱ�� �IJ�������Ϊ��
�IJ��������� ��
�� ������.
������.
���������� ��ֱ�����귽�̣�
��ֱ�����귽�̣�
����ֱ�� ����һ����
����һ���� ������
������ ��
�� ����M��N���㣬��
����M��N���㣬�� ��ֵ��
��ֵ��
��3������С������7�֣�ѡ��4-5������ʽѡ��
��֪ Ϊʵ������
Ϊʵ������
������֤��
������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011����ͨ�����������Ը���ʡ�߿�������ѧ ���ͣ������
�������У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ʒ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������С�
��1������С������7�֣�ѡ��4-2��������任
����� 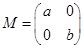 ������a��0��b��0��.
������a��0��b��0��.
��I����a=2��b=3�������M�������M-1��
��II��������C��x2+y2=1�ھ���M����Ӧ�����Ա任�����µõ�����C����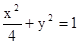 ����a��b��ֵ.
����a��b��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�긣��ʡ�߿���ѧ�Ծ������ƣ��������棩 ���ͣ������
 ������a��0��b��0����
������a��0��b��0����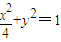 ����a��b��ֵ��
����a��b��ֵ�� ��
�� �����жϵ�P��ֱ��l��λ�ù�ϵ��
�����жϵ�P��ֱ��l��λ�ù�ϵ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com