
【题目】在多面体![]() 中,四边形
中,四边形![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() .
.
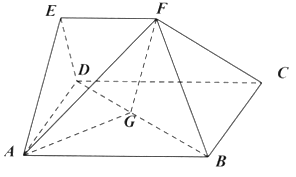
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)证明见解析;(2)答案见解析.
【解析】
(1)由面面垂直的性质定理证明线面垂直即可;
(2)在平面DAE内,过D作AD的垂线DH,以点D为坐标原点,DA,DC,DH所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用平面FAG的法向量和平面EAD的法向量求二面角的余弦值即可确定线段![]() 上是否存在点
上是否存在点![]() .
.
(1)∵平面ADE⊥平面ABCD,平面ADE∩平面ABCD=AD,
正方形中CD⊥AD,∴CD⊥平面ADE.
(2)由(1)知平面ABCD⊥平面AED.
在平面DAE内,过D作AD的垂线DH,则DH⊥平面ABCD,
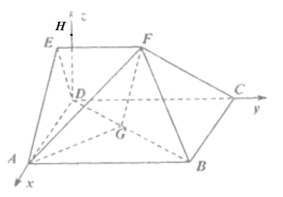
以点D为坐标原点,DA,DC,DH所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设![]() ,则
,则![]() .
.
设平面FAG的一个法向量![]() ,则
,则![]() ,
,
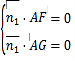 ,即
,即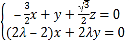 ,
,
令![]() 可得:
可得:![]() ,
,
易知平面EAD的一个法向量![]() ,
,
由已如得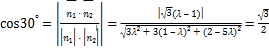 .
.
化简可得:![]() ,即
,即![]() .
.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
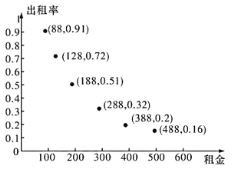
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过曲线C:y![]() x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
(1)求证:x1x2=﹣16;
(2)曲线C分别在点A,B处的切线(与C只有一个公共点,且C在其一侧的直线)交于点M,求点M的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流![]() 类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:
类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)将同一组数据用该区间的中点值作代表,求这100人月薪收入的样本平均数![]() ;
;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间![]() 右侧的每人收取800元;
右侧的每人收取800元;
方案二:每人按月薪收入的样本平均数的![]() 收取;
收取;
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn-n=2(an-2),(n∈N*)
(1)证明:数列{an-1}为等比数列.
(2)若bn=anlog2(an-1),数列{bn}的前项和为Tn,求Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com