
已知函数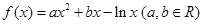
(Ⅰ)设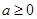 ,求
,求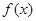 的单调区间;
的单调区间;
(Ⅱ) 设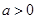 ,且对于任意
,且对于任意 ,
,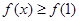 .试比较
.试比较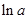 与
与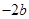 的大小.
的大小.
(Ⅰ) 单调递减区间是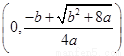 ,单调递增区间是
,单调递增区间是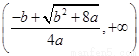
(Ⅱ) 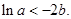
【解析】(Ⅰ)由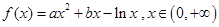 得
得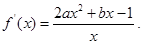
(1)当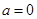 时,
时,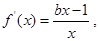
(i)若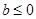 ,当
,当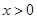 时,
时,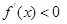 恒成立,
恒成立,
所以函数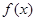 的单调递减区间是
的单调递减区间是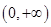 .
.
(ii)若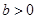 ,当
,当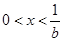 时,
时,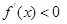 ,函数
,函数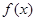 单调递减,
单调递减,
当 时,
时,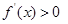 ,函数
,函数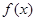 单调递增.
单调递增.
所以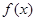 的单调递减区间是
的单调递减区间是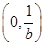 ,单调递增区间是
,单调递增区间是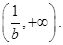
(2)当 时,令
时,令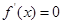 得
得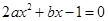 ,
,
由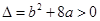 得
得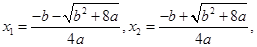
显然
当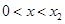 时,
时,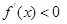 ,函数
,函数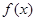 单调递减;
单调递减;
当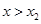 时,
时,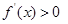 ,函数
,函数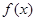 单调递增.
单调递增.
所以函数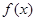 的单调递减区间是
的单调递减区间是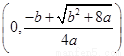 ,
,
单调递增区间是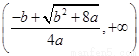 .
.
(Ⅱ)由题意知函数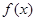 在
在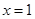 处取得最小值,
处取得最小值,
由(I)知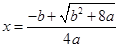 是
是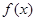 的唯一极小值点,
的唯一极小值点,
故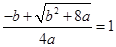 ,整理得
,整理得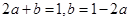 ,
,
令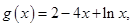 则
则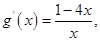
由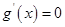 得
得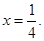
当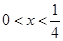 时,
时,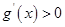 ,
,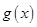 单调递增;
单调递增;
当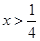 时,
时,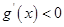 ,
,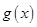 单调递减.
单调递减.
因此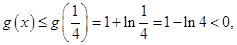
故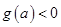 ,即
,即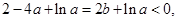
即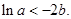
【考点定位】本题考查导数法研究函数的单调性和相关函数值的大小比较,考查分类讨论思想、推理论证能力和运算求解能力.函数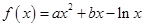 的单调区间判断必然通过导数方法来解决,伴随而来的是关于
的单调区间判断必然通过导数方法来解决,伴随而来的是关于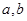 的分类讨论.比较
的分类讨论.比较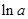 与
与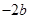 的大小时要根据已知条件和第一问的知识储备,构造新的函数利用单调性直接运算函数值得到结论.本题具备导数研究函数单调性的特征,必然按照程序化运行,即求导、关于参数分类讨论、确定单调区间等步骤进行.而第二问则是在第一问的基础上进一步挖掘解题素材,如隐含条件的发现、新函数的构造等,都为解决问题提供了有力支持.
的大小时要根据已知条件和第一问的知识储备,构造新的函数利用单调性直接运算函数值得到结论.本题具备导数研究函数单调性的特征,必然按照程序化运行,即求导、关于参数分类讨论、确定单调区间等步骤进行.而第二问则是在第一问的基础上进一步挖掘解题素材,如隐含条件的发现、新函数的构造等,都为解决问题提供了有力支持.


科目:高中数学 来源:2012-2013学年辽宁省五校协作体高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数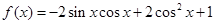
(1)设方程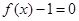 在(0,
在(0,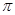 )内有两个零点
)内有两个零点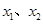 ,求
,求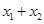 的值;
的值;
(2)若把函数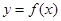 的图像向左移动
的图像向左移动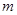
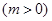 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于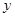 轴对称,求
轴对称,求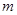 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com