
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩(x) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末成绩(y) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)画出散点图;
(2)计算入学成绩(x)与高一期末成绩(y)的相关关系;
(3)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出一元线性回归方程;
(4)若某学生入学数学成绩为80分,预报他高一期末数学考试成绩.
思路解析:因为问题中最后要求根据入学成绩预报期末成绩,可选择入学成绩x为自变量,期末成绩y为因变量.建立线性关系进行求解.求得回归方程后,将x=80代入即可预报对应的期末成绩.
解:(1)以入学成绩x为自变量,期末成绩y为因变量,作散点图(图略).可以看出,这两组变量有比较好的线性相关关系.
(2)因为![]() (63+67+…+76)=70,
(63+67+…+76)=70,![]() (65+78+…+75)=76.
(65+78+…+75)=76.
∑(xi-![]() )(yi-
)(yi-![]() )=1 894,∑(xi-
)=1 894,∑(xi-![]() )2=2 474,∑(yi-
)2=2 474,∑(yi-![]() )2=2 056.
)2=2 056.
因此求得相关系数为:
r=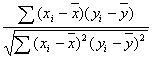 =0.839 8.
=0.839 8.
(3)因为r>r0.05=0.632,这说明数学入学成绩与高一期末期末成绩存在很强的线性相关关系.设线性回归方程为![]() ,在两组变量具有显著的线性关系情况下,
,在两组变量具有显著的线性关系情况下,
![]() =
= ≈0.765 6,
≈0.765 6,![]() =22.410 8.
=22.410 8.
因此所求的线性回归方程是![]() =0.765 6x+22.410 8.
=0.765 6x+22.410 8.
(4)若某学生入学数学成绩为80分,代入上式回归方程可求得,x≈84.即这个学生高一期末数学成绩的预测值为84分.


科目:高中数学 来源: 题型:
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 入学成绩x | 63 | 67 | 75 | 88 | 85 |
| 高一期末成绩y | 65 | 77 | 80 | 82 | 92 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 入学成绩x | 63 | 67 | 75 | 88 | 85 |
| 高一期末成绩y | 65 | 77 | 80 | 82 | 92 |
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
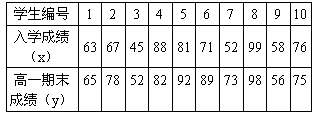
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末成绩y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)计算入学成绩(x)与高一期末考试成绩(y)的相关关系;
(2)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出一元线性回归方程;
(3)若某学生入学数学成绩80分,试估计他高一期末数学考试成绩.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com