练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （湖南卷理2） “成立”是“成立”的(      )

    A．充分不必要条件 B.必要不充分条件 C．充分必要条件  D.既不充分也不必要条件  

    【答案】B

    【解析】由得，由得，所以易知选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （05年湖南卷理）（14分）

    　　    自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，n∈N*，且x1＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成正比，死亡量与xn2成正比，这些比例系数依次为正常数a，b，c.

       （Ⅰ）求xn+1与xn的关系式；

       （Ⅱ）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量保持不变？（不

    要求证明）

    　 （Ⅱ）设a＝2，b＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，则捕捞强度b的

             最大允许值是多少？证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （07年湖南卷理）将杨辉三角中的奇数换成1，偶数换成0，得到如图1所示的0-1三角数表．从上

    往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第次全行的数都为1的是第        行；第61行中1的个数是        ．

    第1行　　　　　 1    1

    第2行         1   0   1

    第3行       1   1   1   1

    第4行     1   0   0   0   1

    第5行   1   1   0   0   1   1

    ……   ………………………………

            　　　　　　　　  图1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （07年湖南卷理）（12分）

    如图2，分别是矩形的边的中点，是上的一点，将，分别沿翻折成，，并连结，使得平面

    平面，，且．连结，如图3．

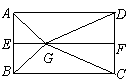
    　　　　图2                            

    图3

    （I）证明：平面平面；

    （II）当，，时，求直线和平面所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (2009湖南卷理)在半径为13的球面上有A , B, C 三点，AB=6，BC=8，CA=10，则          

    （1）球心到平面ABC的距离为 12  ；

    （2）过Ａ，B两点的大圆面为平面ABC所成二面角为（锐角）的正切值为   3  

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (2009湖南卷理)在半径为13的球面上有A , B, C 三点，AB=6，BC=8，CA=10，则          

    （1）球心到平面ABC的距离为 12  ；

    （2）过Ａ，B两点的大圆面为平面ABC所成二面角为（锐角）的正切值为   3  

    查看答案和解析>>

    同步练习册答案